
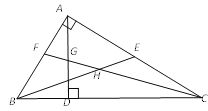
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于G,交BE于H.下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中所有正确结论的序号是
A.①②③④B.①②③C.②④D.①③
【答案】B
【解析】
根据等底等高的三角形的面积相等即可判断①;根据三角形内角和定理求出∠ABC=∠CAD,根据三角形的外角性质即可推出②;根据三角形内角和定理求出∠FAG=∠ACD,根据角平分线定义即可判断③;根据等腰三角形的判定判断④即可.
解:∵BE是中线,
∴AE=CE,
∴S△ABE=S△BCE(等底等高的三角形的面积相等),故①正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故②正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故③正确;
根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故④错误;
故选B.


科目:初中数学 来源: 题型:
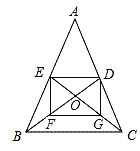
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
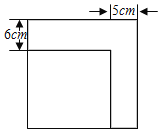
【题目】如图,小刚将一个正方形纸片剪去一个宽为5cm的长条后,再从剩下的长方形纸片上剪去一个宽为6cm的长条.如果两次剪下的长条面积正好相等,求两个所剪下的长条的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某班35名学生投篮成绩的条形图,其中上面部分数据破损导致数据不完全,已知此班学生投篮成绩的中位数是5,下列选项正确的是_______.
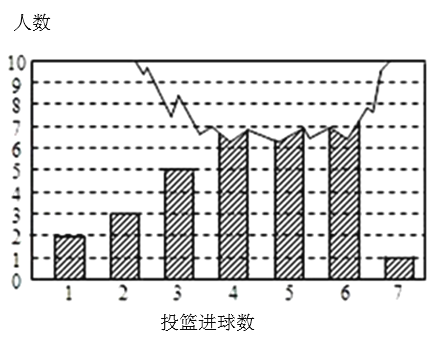
①3球以下(含3球)的人数;②4球以下(含4球)的人数; ③5球以下(含5球)的人数;④6球以下(含6球)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列推理所注理由正确的是( )
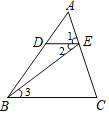
A.∵DE∥BC,∴∠1=∠C(同位角相等,两直线平行)
B.∵∠2=∠3,∴DE∥BC(两直线平行,内错角相等)
C.∵DE∥BC,∴∠2=∠3(两直线平行,内错角相等)
D.∵∠DEC+∠C=180°,∴DE∥BC(同旁内角相等,两直线平行)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,点M,N分别是AB,CD上两点,点G在AB,CD之间.
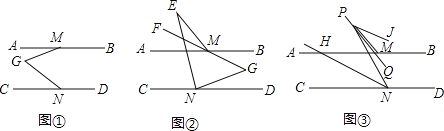
(1)求证:∠AMG+∠CNG=∠MGN;
(2)如图②,点E是AB上方一点,MF平分∠AME,若点G恰好在MF的反向延长线上,且NE平分∠CNG,2∠E+∠G=90°,求∠AME的度数;
(3)如图③,若点P是(2)中的EM上一动点,PQ平分∠MPQ.NH平分∠PNC,交AB于点H,PJ∥NH,直接写出∠JPQ的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别从两个班级中随意抽取甲、乙两组各10名学生,他们的数学测验成绩(单位:分)如下:

计算甲、乙两组学生数学测验成绩的平均数、标准差和方差,哪个班级学生的成绩比较整齐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个整数N,可以用一个多项式来表示:
![]() ,例如:325=3×102+2×10+5.
,例如:325=3×102+2×10+5.
一个正两位数的个位数字是x,十位数字是y.
(1)把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数,试说明新数与原数的和能被11整除;
(2)若![]() 试求出符合条件的所有两位数.
试求出符合条件的所有两位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com