
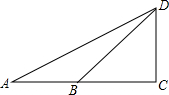
 小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.
小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.科目:初中数学 来源: 题型:解答题
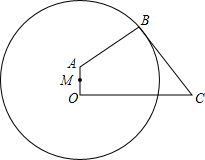 如图,为了保护运河入江口的古桥OA,规划建一座新桥BC,已知,古桥OA与河岸OC垂足,新桥BC与河岸AB垂直,且BC=AB,OC=210m,tan∠BCO=$\frac{4}{3}$.
如图,为了保护运河入江口的古桥OA,规划建一座新桥BC,已知,古桥OA与河岸OC垂足,新桥BC与河岸AB垂直,且BC=AB,OC=210m,tan∠BCO=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 现有一张圆心角为108°,半径为40cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ的大小是( )
现有一张圆心角为108°,半径为40cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ的大小是( )| A. | 18° | B. | 36° | C. | 72° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{2}{3}$$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),将△AOB绕点A逆时针旋转90°得到△AEF,则点B的对应点F的坐标是( )
如图,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),将△AOB绕点A逆时针旋转90°得到△AEF,则点B的对应点F的坐标是( )| A. | (3,-1) | B. | (3,3) | C. | (-3,7) | D. | (0,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为1或$\frac{\sqrt{3}}{3}$.
如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为1或$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y=x2+bx+c图象顶点为C,与直线y=x+m图象交于AB两点,其中A点的坐标为(3,4),B点在y轴上.
如图,已知二次函数y=x2+bx+c图象顶点为C,与直线y=x+m图象交于AB两点,其中A点的坐标为(3,4),B点在y轴上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com