【题目】如图，在平面直角坐标系中，将正方形
绕点
逆时针旋转
后得到正方形
，依此方式，绕点连续旋转2019次得到正方形
，如果点
的坐标为（1，0），那么点
的坐标为________．
【答案】
【解析】
根据图形可知：点B在以O为圆心,以OB为半径的圆上运动,由旋转可知：将正方形OABC绕点O逆时针旋转45后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45，可得对应点B的坐标，根据规律发现是8次一循环，可得结论.
∵四边形OABC是正方形，且OA=1，∴B(1,1),连接OB，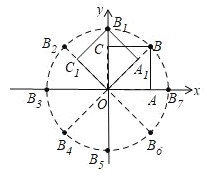
由勾股定理得：OB=
，
由旋转得：OB=OB1=OB2=OB3=…=，
∵将正方形OABC绕点O逆时针旋转45后得到正方形OA1B1C1，
相当于将线段OB绕点O逆时针旋转45,依次得到∠AOB=∠BOB1=∠B1OB2=…=45，
∴B1(0,
),B2(1,1),B3(,0)，…，
发现是8次一循环，所以2019÷8=252…3，
∴点B2019的坐标为(,0)
世纪百通期末金卷系列答案科目：初中数学 来源： 题型：
【题目】如图AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连结AC、OC、BC.
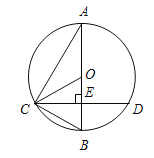
（1）求证：∠ACO=∠BCD;
（2）若EB=2cm，CD=8m，求⊙O的直径.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某小区有一长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们面积之和为60平方米，两块绿地之间及周边留有宽度相等的人行通道，则人行道的宽度为（ ）米．
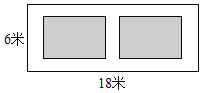
A. 2B. 1C. 8或1D. 8
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明的纸箱里有分别标有汉字“热”“爱”“祖”“国”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先摇匀再摸球.
（1）若从中任取一个球，求摸出球上的汉字刚好是“国”字的概率.
（2）小红从中任取球，不放回，再从中任取一球，请用树状图或列表法，求小红取出的两个球上的汉字恰好能组成“爱国”或“祖国”的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，小正方形网格的边长为 1个单位长度，△ABC的三个顶点的坐标分别为A（﹣3，4），B（﹣5，2），C（﹣2，1）．
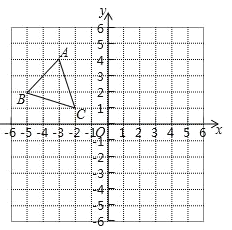
（1）画出
关于
轴对称的图形
并写出点
的坐标；
（2）将绕点O逆时针旋转
，画出旋转后的
,并写出点
的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，利用一个直角墙角修建一个梯形储料场ABCD，其中∠C＝120°．若新建墙BC与CD总长为12m，则该梯形储料场ABCD的最大面积是（ ）
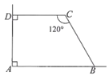
A.18m2B.
m2C.
m2D.
m2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题，“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问锯几何？”用现代的数学语言表述是：“如图，CD为⊙O的直径，弦AB⊥CD垂足为E，CE=1寸，AB=10寸，求直径CD的长”，依题意，CD长为（ ）
A．12寸 B．13寸 C．24寸 D．26寸
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
与
轴交于点
，对称轴为直线
，与
轴交点
在
和
之间（包含这两个点）运动，有如下四个结论：
①抛物线与轴的另一个交点是
；
②点
，
在抛物线上，且满足
，则
；
③常数项
的取值范围是
；
④系数
的取值范围是
.
上述结论中所有正确结论的序号是（ ）
A.①②③B.②③④C.①③D.①③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线y＝﹣5x+5与x轴、y轴分别交于A，C两点，抛物线y＝x2+bx+c经过A，C两点，与x轴交于另一点B．
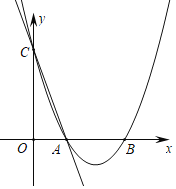
（1）求抛物线解析式及B点坐标；
（2）x2+bx+c≤﹣5x+5的解集是 ；
（3）若点M为抛物线上一动点，连接MA、MB，当点M运动到某一位置时，△ABM面积为△ABC的面积的
倍，求此时点M的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com