
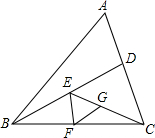
 如图,△ABC的面积为32cm2,点D、E、F、G分别为AC,BD,BC,EC的中点,则△EFG的面积为2cm2.
如图,△ABC的面积为32cm2,点D、E、F、G分别为AC,BD,BC,EC的中点,则△EFG的面积为2cm2. 分析 根据三角形中线把三角形分成两个面积相等的三角形可得S△ABD=S△BCD=$\frac{1}{2}$S△ABC,S△BCE=$\frac{1}{2}$S△BCD,S△CEF=$\frac{1}{2}$S△BCE,S△EFG=$\frac{1}{2}$S△CEF,再根据S△EFG=$\frac{1}{2}$S△CEF=$\frac{1}{16}$S△ABC计算即可得解.
解答  解:∵D是AC的中点,
解:∵D是AC的中点,
∴S△ABD=S△BCD=$\frac{1}{2}$S△ABC,
∵E是BD的中点,
∴S△BCE=$\frac{1}{2}$S△BCD=$\frac{1}{4}$S△ABC,
∵F是BC的中点,
∴S△CEF=$\frac{1}{2}$S△BCE=$\frac{1}{8}$S△ABC,
∵G是EC的中点,
∴S△EFG=$\frac{1}{2}$S△CEF=$\frac{1}{16}$S△ABC,
∵△ABC的面积为32cm2,
∴△EFG的面积=$\frac{1}{16}$×32=2cm2.
故答案为:2cm2.
点评 本题考查了三角形的面积主要利用了三角形中线把三角形分成两个面积相等的三角形,理论依据是等底等高的三角形的面积相等,需熟记.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
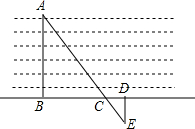 如图,要测量河岸相对的两点A、B的距离,先从点B出发与AB成90°角方向,向前走50m到C处立一根标杆,然后方向不变继续朝前走10m到D处,在D处转90°沿DE方向再走17m,这时A、C、E在同一直线上.问A、B间的距离约为多少?
如图,要测量河岸相对的两点A、B的距离,先从点B出发与AB成90°角方向,向前走50m到C处立一根标杆,然后方向不变继续朝前走10m到D处,在D处转90°沿DE方向再走17m,这时A、C、E在同一直线上.问A、B间的距离约为多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
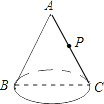 如图,有一个圆锥,它的底面半径是2cm,母线长是8cm,在点B处有一只蚂蚁,它想吃到与B点相对且离圆锥顶点3$\sqrt{2}$cm 的点P处的食物,蚂蚁爬行的最短路程是2$\sqrt{5}$cm.
如图,有一个圆锥,它的底面半径是2cm,母线长是8cm,在点B处有一只蚂蚁,它想吃到与B点相对且离圆锥顶点3$\sqrt{2}$cm 的点P处的食物,蚂蚁爬行的最短路程是2$\sqrt{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com