
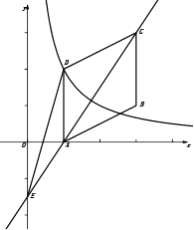
【题目】(本题满分10分)如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=![]() (k≠0,x>0)过点D.
(k≠0,x>0)过点D.
(1)求此双曲线的解析式;
(2)作直线AC交y轴于点E,连结DE,求△ CDE的面积.
【答案】(1)![]() ;(2)3.
;(2)3.
【解析】试题分析:(1)根据在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),可以求得点D的坐标,又因为双曲线![]() (k≠0,x>0)过点D,从而可以求得k的值,从而可以求得双曲线的解析式;
(k≠0,x>0)过点D,从而可以求得k的值,从而可以求得双曲线的解析式;
(2)由图可知三角形CDE的面积等于三角形EDA与三角形ADC的面积之和,从而可以解答本题.
试题解析:(1)∵在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),∴点D的坐标是(1,2),∵双曲线![]() (k≠0,x>0)过点D,∴2=
(k≠0,x>0)过点D,∴2=![]() ,得k=2,即双曲线的解析式是:
,得k=2,即双曲线的解析式是: ![]() ;
;
(2)∵直线AC交y轴于点E,∴S△CDE=S△EDA+S△ADC=![]() =1+2=3,即△CDE的面积是3.
=1+2=3,即△CDE的面积是3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,已知函数y1=![]() (x>0)与y2=﹣
(x>0)与y2=﹣![]() (x<0)的图象如图所示,点A、B是函数y1=
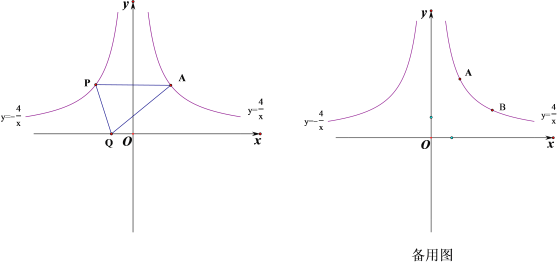
(x<0)的图象如图所示,点A、B是函数y1=![]() (x>0)图象上的两点,点P是y2=﹣
(x>0)图象上的两点,点P是y2=﹣![]() (x<0)的图象上的一点,且AP∥x轴,点Q是x轴上一点,设点A、B的横坐标分别为m、n(m≠n).
(x<0)的图象上的一点,且AP∥x轴,点Q是x轴上一点,设点A、B的横坐标分别为m、n(m≠n).
(1)求△APQ的面积;
(2)若△APQ是等腰直角三角形,求点Q的坐标;
(3)若△OAB是以AB为底的等腰三角形,求mn的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:△ABC内接于⊙O,点D在OC的延长线上,sinB=![]() ,∠D=30度.
,∠D=30度.
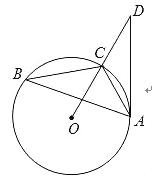
(1)求证:AD是⊙O的切线;
(2)若AC=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A.抛物线y=﹣x2+x的开口向下
B.两点之间线段最短
C.角平分线上的点到角两边的距离相等
D.一次函数y=﹣x+1的函数值随自变量的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
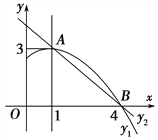
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;
②abc>0;
③方程ax2+bx+c=3有两个相等的实数根;
④抛物线与x轴的另一个交点是(-1,0);
⑤当1<x<4时,有y2<y1,
其中正确的是( ).
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列推理过程,在括号中填写理由.
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
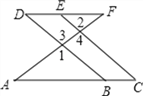
解:∵∠1=∠2(已知),∠1=∠3(______________),
∴∠2=∠3(___________________).
∴__∥__(__________________________________).
∴∠C=∠ABD (________________________________).
又∵∠C=∠D(____________),
∴∠D=∠ABD(等量代换)
∴AC∥DF(______________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面几何的学习过程中,我们经常会研究角和线之间的关系.
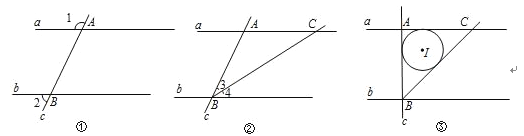
(1)如图①,直线a、b被直线c所截,交点分别为A、B.当∠1、∠2满足数量关系 时,a∥b;
(2)如图②,在(1)中,作射线BC,与直线a的交点为C,当∠3、∠4满足何种数量关系时,AB=AC?证明你的结论;
(3)如图③,在(2)中,若∠BAC=90°,AB=2,⊙I为△ABC的内切圆.
①求⊙I的半径;
②P为直线a上一点,若⊙I上存在两个点M、N,使∠MPN=60°,直接写出AP长度的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com