
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标 ,点B1的坐标 ;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标 .

科目:初中数学 来源: 题型:
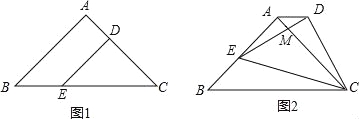
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=2![]() ,D、E两点分别在AC、BC上,且DE∥AB,DC=2
,D、E两点分别在AC、BC上,且DE∥AB,DC=2![]() ,将△CDE绕点C顺时针旋转得到△CD′E′,如图2,点D、E对应点分别为D′、E′、D′、E′与AC相交于点M,当E′刚好落在边AB上时,△AMD′的面积为 .
,将△CDE绕点C顺时针旋转得到△CD′E′,如图2,点D、E对应点分别为D′、E′、D′、E′与AC相交于点M,当E′刚好落在边AB上时,△AMD′的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果M个不同的正整数,对其中的任意两个数,这两个数的积能被这两个数的和整除,则称这组数为M个数的祖冲之数组.如(3,6)为两个数的祖冲之数组,因为3×6能被(3+6整除);又如(15,30,60)为三个数的祖冲之数组,因为(15×30)能被(15+30)整除,(15×60)能被(15+60)整除,(30×60)能被(30+60)整除…
(1)我们发现,3和6,4和12,5和20,6和30…,都是两个数的祖冲之数组;由此猜测n和n(n﹣1)(n≥2,n为整数)组成的数组是两个数的祖冲之数组,请证明这一猜想.
(3)若(4a,5a,6a)是三个数的祖冲之数组,求满足条件的所有三位正整数a.
查看答案和解析>>
科目:初中数学 来源: 题型:
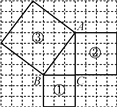
【题目】如图,正方形网格中,每个小正方形的边长都为 1.
(1)正方形①的面积 S1=_________cm2 ,正方形②的面积 S2=______________cm2,正方形③的面积S3=____cm2;
(2)S1,S2,S3之间存在什么关系?
(3)猜想:如果Rt△ABC的三边BC,AC,AB的长分别为a,b,c,那么它们之间存在什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
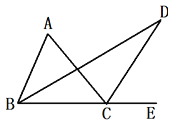
【题目】在ΔABC中,∠ABC的平分线与在∠ACE的平分线相交于点D.
(1)若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数.
(2)由(1)小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,∠BOC=30°,射线OM平分∠AOC,ON平分∠BOC. 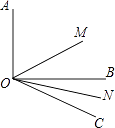
(1)求∠MON的度数;
(2)如果(1)中,∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)的结果中,你能看出什么规律?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com