
【题目】如图,已知一次函数y=kx+4图象交直线OA于点A(1,2),交y轴于点B,点C为坐标平面内一点.
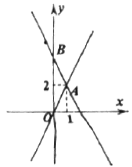
(1)求k值;
(2)若以O、A、B、C为顶点的四边形为菱形,则C点坐标为 ;
(3)在直线AB上找点D,使△OAD的面积与((2)中菱形面积相等,则D点坐标为 .
【答案】(1)k=-2;(2) (-1,2);(3)(-1,6)或(3,-2)
【解析】
(1)利用待定系数法即可解决问题;
(2)只要证明A、C关于y轴对称即可解决问题;
(3)分两种情形,根据AD=2AB即可解决问题;
(1)将点A(1,2)代入一次函数y=kx+4中,
2=k+4,得k=-2.
(2)∵一次函数解析式为y=-2x+4,
∴B点坐标为(0,4),∵A(1,2),
∴OA=![]() ,AB=
,AB=![]() ,
,
∵以O、A、B、C为顶点的四边形为菱形,
∴存在OB⊥AC,且OB、AC互相平分,由对称性得C点坐标为(-1,2).
故答案为(-1,2).
(3)∵四边形OABC是菱形,
∴S△OAB=![]() S菱形ABCO,
S菱形ABCO,
∴当AD=2AB时,△OAD的面积与(2)中菱形面积相等,
∵一次函数y=-2x+4与x轴的交点为(2,0),
∴D(-1,6)或(3,-2).


科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AB的垂直平分线DE分别交AB、AC于D、E.
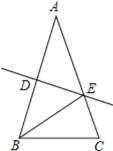
(1)若AC=12,BC=10,求△EBC的周长;
(2)若∠A=40°,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙仓库共存放某种原料450吨,如果运出甲仓库所存原料的60%,乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将300吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为120元/吨和100元/吨.经协商,从甲仓库到工厂的运价可优惠a元吨(10≤a≤30),从乙仓库到工厂的运价不变,设从甲仓库运m吨原料到工厂,请求出总运费W关于m的函数解析式(不要求写出m的取值范围);
(3)在(2)的条件下,请根据函数的性质说明:随着m的增大,W的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP、BQ、PQ.
(1)求证:△APD≌△BQC;
(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙仓库共存放某种原料450吨,如果运出甲仓库所存原料的60%,乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将300吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为120元/吨和100元/吨.经协商,从甲仓库到工厂的运价可优惠a元吨(10≤a≤30),从乙仓库到工厂的运价不变,设从甲仓库运m吨原料到工厂,请求出总运费W关于m的函数解析式(不要求写出m的取值范围);
(3)在(2)的条件下,请根据函数的性质说明:随着m的增大,W的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( )
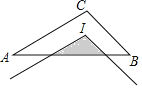
A. 4.5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解七年级![]() 名学生其中数学考试情况,从中抽取了
名学生其中数学考试情况,从中抽取了![]() 名学生的数学成绩进行了统计,下面
名学生的数学成绩进行了统计,下面![]() 个判断中正确的有( )个.
个判断中正确的有( )个.
①这种调查的方式是抽样调查;②![]() 名学生是总体;③每名学生的数学成绩是个体;④
名学生是总体;③每名学生的数学成绩是个体;④![]() 名学生是总体的一个样本;⑤样本容量是
名学生是总体的一个样本;⑤样本容量是![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
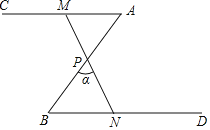
【题目】如图,∠A=∠B=50°,P为AB中点,点M为射线AC上(不与点A重合)的任意点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若△BPN的外心在该三角形的内部,直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
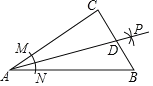
【题目】如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若AC=24,AB=30,且
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若AC=24,AB=30,且![]() =216,则△ABD的面积是( )
=216,则△ABD的面积是( )
A.105B.120
C.135D.115
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com