
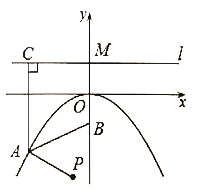
【题目】如图,抛物线![]() 经过点
经过点![]() .点
.点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,点
轴,点![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 于点
于点![]() .
.
![]() 求抛物线解析式:
求抛物线解析式:
![]() 在抛物线对称轴上是否存在一定点
在抛物线对称轴上是否存在一定点![]() ,使得
,使得![]() 永远成立?若存在,求出点
永远成立?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 若点
若点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),交
的左边),交![]() 轴正半轴于点
轴正半轴于点![]() .
.
(1)如图1,当![]() 时.
时.
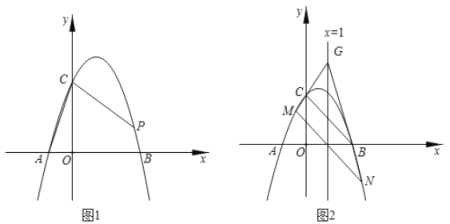
①直接写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
②若抛物线上有一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
(2)如图2,平移直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 在定直线
在定直线![]() 上运动,求
上运动,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,![]() ,BE是AC边上的中线,点D在射线BC上.
,BE是AC边上的中线,点D在射线BC上.
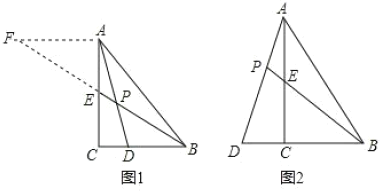
(1)如图1,点D在BC边上,![]() ,AD与BE相交于点P,过点A作
,AD与BE相交于点P,过点A作![]() ,交BE的延长线于点F,易得
,交BE的延长线于点F,易得![]() 的值为 ;
的值为 ;
(2)如图2,在△ABC中,![]() ,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,
,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若CD=2,AC=6,则BP= .
查看答案和解析>>
科目:初中数学 来源: 题型:
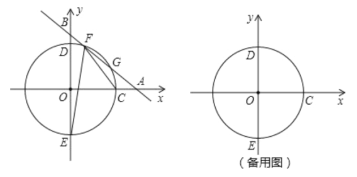
【题目】如图,平面直角坐标系![]() 中,一次函数
中,一次函数![]() (
(![]() 为常数,
为常数,![]() )的图像与
)的图像与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() ,半径为4的⊙
,半径为4的⊙![]() 与
与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 在点
在点![]() 上方.
上方.
(1)若直线![]() 与弧
与弧![]() 有两个交点
有两个交点![]() .
.
①求![]() 的度数;
的度数;
②用含![]() 的代数式表示
的代数式表示![]() ,并直接写出
,并直接写出![]() 的取值范围;
的取值范围;
(2)设![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ?若存在,请求出
?若存在,请求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
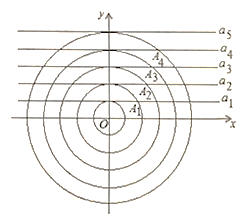
【题目】如图所示,在平面直角坐标系中,一组同心圆的圆心为坐标原点![]() ,它们的半径分别为
,它们的半径分别为![]() .按照“加
.按照“加![]() "依次递增; 一组平行线
"依次递增; 一组平行线![]() , ..分别过
, ..分别过![]() ,且与过该点的圆相切.若半径为
,且与过该点的圆相切.若半径为![]() 的圆与
的圆与![]() 在第一象限内交于点
在第一象限内交于点![]() ,半径为
,半径为![]() 的圆与
的圆与![]() 在第象限内相交于点
在第象限内相交于点![]() ,半径为
,半径为![]() 的圆与
的圆与![]() 在第一象限内相交于点
在第一象限内相交于点![]() 按照此规律,则点
按照此规律,则点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)用配方法求它的顶点坐标、对称轴;
(2)当![]() 的值在什么范围内时,
的值在什么范围内时,![]() 随
随![]() 的增大而增大?当
的增大而增大?当![]() 的值在什么范围内时,
的值在什么范围内时,![]() 随
随![]() 的增大而减小?
的增大而减小?
(3)当![]() 的值在什么范围内时,抛物线在
的值在什么范围内时,抛物线在![]() 轴上方?
轴上方?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,![]() ,AC=4,BC=3,点D是斜边AB的中点. 以点D为顶点作
,AC=4,BC=3,点D是斜边AB的中点. 以点D为顶点作![]() ,射线DM、DN分别交边AC、CB于点E、F.
,射线DM、DN分别交边AC、CB于点E、F.
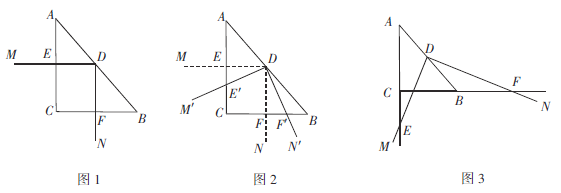
特例
(1)如图1,若![]() ,不添加辅助线,图1中所有与△ABC相似的三角形为 ,
,不添加辅助线,图1中所有与△ABC相似的三角形为 ,![]() ;
;
操作探究:
(2)将(1)中的![]() 从图1 的位置开始绕点D按逆时针方向旋转,得到
从图1 的位置开始绕点D按逆时针方向旋转,得到![]() .如图2,当射线
.如图2,当射线![]() 分别交边
分别交边![]() 于点
于点![]() 时,求
时,求![]() 的值;
的值;
拓展延伸:
(3)如图3,![]() 中,
中,![]() ,AC=m,BC=n,点D是斜边AB的中点,以点D为顶点作
,AC=m,BC=n,点D是斜边AB的中点,以点D为顶点作![]() ,射线
,射线![]() 分别交边
分别交边![]() 的延长线于点
的延长线于点![]() ,则
,则![]() 的值为_______________.(用含
的值为_______________.(用含![]() 的代数式表示,直接回答即可)
的代数式表示,直接回答即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
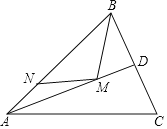
【题目】如图,在锐角△ABC中,AB=5![]() ,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD,AB上的动点,则BM+MN的最小值是______.
,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD,AB上的动点,则BM+MN的最小值是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com