
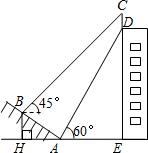
 如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知sin∠BAH=$\frac{1}{2}$,AB=10米,AE=15米.
如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知sin∠BAH=$\frac{1}{2}$,AB=10米,AE=15米.分析 (1)根据正弦的概念求出BH的长;
(2)在△ADE解直角三角形求出DE的长,进而可求出EH即BG的长,在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长然后根据CD=CG+GE-DE即可求出广告牌的高度.
解答 解:(1)由题意得,sin∠BAH=$\frac{BH}{AB}$=$\frac{1}{2}$,又AB=10米,
∴BH=$\frac{1}{2}$AB=5米;
(2))∵BH⊥HE,GE⊥HE,BG⊥DE,
∴四边形BHEG是矩形.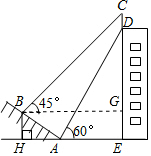
∵由(1)得:BH=5,AH=5$\sqrt{3}$,
∴BG=AH+AE=5$\sqrt{3}$+15,
Rt△BGC中,∠CBG=45°,
∴CG=BG=5$\sqrt{3}$+15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE=$\sqrt{3}$AE=15$\sqrt{3}$.
∴CD=CG+GE-DE=5$\sqrt{3}$+15+5-15$\sqrt{3}$=20-10$\sqrt{3}$.
答:广告牌CD的高度为(20-10$\sqrt{3}$)米.
点评 此题综合考查了仰角、坡度的定义,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日 期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化(万人) | +0.5 | +0.7 | +0.8 | -0.4 | -0.6 | +0.2 | -0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
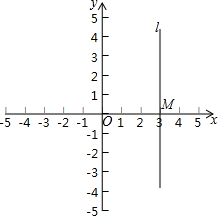 如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com