
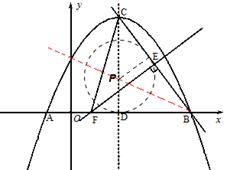
如图23,已知抛物线![]() 与
与![]() 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线![]() ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1.
1.填空:![]() =_______。
=_______。![]() =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______):
2.若线段BC的垂直平分线EF交BC于点E,交![]() 轴于点F.求FC的长;
轴于点F.求FC的长;
3.探究:在抛物线的对称轴上是否存在点P,使⊙P与![]() 轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。

1.![]() ,
,![]() ,5,0。
,5,0。
2.由(1)得抛物线的解析式为![]() ,化为顶点式为
,化为顶点式为![]() 。
。
∴C(2,4)。
∵E为BC的中点,由中点坐标公式求得E的坐标为(3.5,2),……………………………..3分
设直线BC的表达式为![]() ,则
,则![]() ,解得
,解得![]() 。
。
∴直线BC的表达式为![]() 。……………………………………………………………5分
。……………………………………………………………5分
设直线EF的表达式为![]() ,
,
∵EF为BC的中垂线,∴EF⊥BC。∴由相似可得![]() ,即直线EF的表达式为
,即直线EF的表达式为![]() 。
。
把E(3.5,2)代入得 ![]() ,解得
,解得![]() 。
。
∴直线EF的表达式为![]() 。……………………………………7分
。……………………………………7分
在 ![]() 中,令
中,令![]() =0,得
=0,得![]() ,解得
,解得![]() 。∴F(
。∴F(![]() ,0)。
,0)。
∴FC=FB=5-![]() 。答:FC的长是
。答:FC的长是![]() 。……………………………8分
。……………………………8分
3.存在。作∠OBC的平分线交DC于点P,则P满足条件。
设P(2,![]() ),则P到
),则P到![]() 轴的距离等于P到直线BC的距离,都是|
轴的距离等于P到直线BC的距离,都是|![]() |。
|。
∵点C的坐标是(2,4),点B的坐标是(5,0),
∴CD=4,DB=5-2=3。∴BC= ![]() 。
。
∴sin∠BCD=![]() 。……………………………………………………………………10分
。……………………………………………………………………10分
当点P在![]() 轴上方时,得
轴上方时,得![]() ,解得
,解得![]() 。点P的坐标是(2,
。点P的坐标是(2,![]() )。
)。
当点P在![]() 轴下方时,得
轴下方时,得![]() ,解得
,解得![]() 。点P的坐标是(2,-6)。
。点P的坐标是(2,-6)。
∴在抛物线的对称轴上存在点P,使⊙P与x轴、直线BC都相切,
点P的坐标是(2,![]() ),(2,-6 )。………………………………………………………12分
),(2,-6 )。………………………………………………………12分
解析:(1)根据对称轴和OA=1求出A、B的坐标,代入解析式求出b、c即可;
(2)求出C(2,4)求得E的坐标为(3.5,2)和直线BC的表达式为y=-![]() x+
x+![]() ,设直线EF的表达式为y=kx+b,根据EF为BC的中垂线求出k=
,设直线EF的表达式为y=kx+b,根据EF为BC的中垂线求出k=![]() 和b=-
和b=-![]() 推出直线EF的表达式为y=
推出直线EF的表达式为y=![]() x-
x-![]() ,令y=0,得x=
,令y=0,得x=![]() 即可求出答案;
即可求出答案;
(3)作∠OBC的平分线交DC于点P,设P(2,a),根据抛物线解析式求出顶点C的坐标与点B的坐标,然后利用∠BCD的正弦列式即可求解


科目:初中数学 来源: 题型:
| 3 |
| 3 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 与
与 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线 ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1. =_______。
=_______。 =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______): 轴于点F.求FC的长;
轴于点F.求FC的长; 轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2012届山东省宁津县实验中学九年级中考模拟数学试卷(带解析) 题型:解答题
如图23,已知抛物线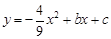 与
与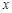 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线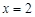 ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1.
【小题1】填空: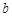 =_______。
=_______。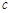 =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______):
【小题2】若线段BC的垂直平分线EF交BC于点E,交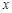 轴于点F.求FC的长;
轴于点F.求FC的长;
【小题3】探究:在抛物线的对称轴上是否存在点P,使⊙P与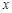 轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省九年级中考模拟数学试卷(解析版) 题型:解答题
如图23,已知抛物线 与
与 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线 ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1.
1.填空: =_______。
=_______。 =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______):
2.若线段BC的垂直平分线EF交BC于点E,交 轴于点F.求FC的长;
轴于点F.求FC的长;
3.探究:在抛物线的对称轴上是否存在点P,使⊙P与 轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com