
����Ŀ��ѧ����ѧϰ��Ȥ�����ÿλ��ʦ�dz���ע�����⣮Ϊ�ˣ�ijУ��ʦ�Ը�У����ѧ����ѧϰ��Ȥ������һ�γ������飨��ѧ����ѧϰ��Ȥ��Ϊ������Σ�A��Σ��ܸ���Ȥ��B��Σ��ϸ���Ȥ��C��Σ�������Ȥ�����������������Ƴ���ͼ�ٺ�ͼ�ڵ�ͳ��ͼ�������������������ͼ���ṩ����Ϣ������������⣺
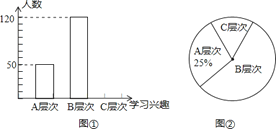
��1���˴γ��������У��������� ��ѧ����
��2����ͼ�ٲ���������
��3����ͼ����C����������ε�Բ�ĽǵĶ�����
��4�����ݳ�������Ľ����������Ƹ�У1200��ѧ���д�Լ�ж�����ѧ����ѧϰ����Ȥ������A��κ�B��Σ���
���𰸡���1��200����2������������3��54�� ����4��1020
��������
��1����ͼ��֪A��ε�������50����ͼ��֪A�����ռ�İٷֱ���25%����˴γ��������У��������������=![]()
��2��C��ε�����Ϊ��200-120-50=30���ˣ���
��ͼ��

��3��C����������ε�Բ�ĽǵĶ����ǣ�360��15%=54����
��4����������ã���25%+60%����1200=1020���ˣ�
�𣺹��Ƹ�У1200��ѧ���д�Լ��1020��ѧ����ѧϰ����Ȥ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
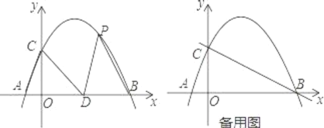
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+2������A(��1��0)�͵�B(4��0)������y�ύ�ڵ�C����D������Ϊ(2��0)����P(m��n)�Ǹ��������ϵ�һ�����㣬����CA��CD��PD��PB��
(1)��������ߵĽ���ʽ��
(2)����PDB��������ڡ�CAD�����ʱ�����P�����ꣻ
(3)��m��0��n��0ʱ������P��ֱ��PE��y���ڵ�E��ֱ��BC�ڵ�F������F��FG��x���ڵ�G������EG����ֱ��д�����ŵ�P���˶����߶�EG����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶��1����ȫ��50��ͬѧ��������ͬ����Ȥ����С�飬ÿ�˶��μ���ֻ�ܲμ�һ��С�飬ͳ�ƣ�����ȫ���������±���
��� | һ | �� | �� | �� | �� |
���� |
| 15 | 20 | 10 |
|
��֪ǰ������С�������֮����![]() ��
��
����������⣺
��1��![]() �� ��
�� ��
��2����ȫ����ͳ��ͼ��
��3�����ӵ�һ��͵���������ѡ����ͬѧ����������ͬѧ��ͬһ��ĸ��ʣ�������״ͼ���б������п��ܶ��г�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
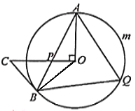
����Ŀ����ͼ��AB����O���ң�����O��OC��OA��OC����AB��P����CP=CB��
��1����֤��BC����O�����ߣ�
��2����֪��BAO=25������Q�ǻ�AmB�ϵ�һ��.
������AQB�Ķ�����
����OA=18����AmB�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ���ı���ABCD�У�AB��10��BC��16��cosB��![]() ����P�DZ�BC�ϵĶ��㣬��CPΪ�뾶��ԲC���AD���ڵ�E��F����F�ڵ�E���Ҳࣩ������CE������BA���ڵ�G��
����P�DZ�BC�ϵĶ��㣬��CPΪ�뾶��ԲC���AD���ڵ�E��F����F�ڵ�E���Ҳࣩ������CE������BA���ڵ�G��
��1����ԲC������Aʱ����CP�ij�
��2������AP����AP//CGʱ������EF�ij�
��3������AGE�ǵ���������ʱ����ԲC�İ뾶����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������֣���ͼ����E��F�ֱ���������ABCD�ı�BC��CD�ϣ�����EF����ΪAB=AD�����Ѧ�ABE��A��ʱ����ת90������ADG����ʹAB��AD�غϣ���Ϊ��CDA=��B=90�㣬���ԡ�FDG=180�㣬����F��D��G���ߣ�
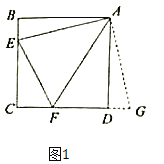
���__________����һ�����������ɵæ�AEF�զ�AGF��������һ���о����ǿ��Է��֣���BE��EF��FD����__________ʱ����EAF=45�㣮
��Ӧ�ã�
��ͼ���ھ���ABCD�У�AB=6��AD=m����E�ڱ�BC�ϣ���BE=2��
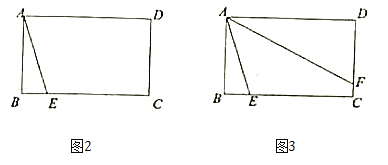
��1����m=8����F�ڱ�DC�ϣ��ҡ�EAF=45�㣨��ͼ������DF�ij���
��2������F�ڱ�DC�ϣ��ҡ�EAF=45�㣬��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ���ACB=90������E��F�ֱ��DZ�BC��AC���е㣬P��AB��һ�㣬��PFΪһֱ�DZ�������ֱ��������PFQ���ҡ�FPQ=90������AB=10��PB=1����QE��ֵΪ��������

A. 3 B. 3![]() C. 4 D. 4
C. 4 D. 4![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
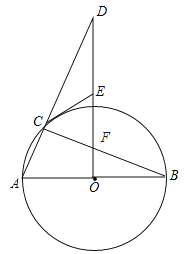
����Ŀ����ͼ��![]() ��
��![]() ֱ����
ֱ����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �����߽�
�����߽�![]() �ڵ�
�ڵ�![]() ����
����![]() �ӽ�
�ӽ�![]() �ڵ�
�ڵ�![]()
��1����֤��![]()
��2������![]() ���ӳ�����
���ӳ�����![]() �ڵ�
�ڵ�![]() ����գ�
����գ�
�ٵ�![]() �Ķ���Ϊ_________ʱ���ı���
�Ķ���Ϊ_________ʱ���ı���![]() Ϊ���Σ�
����
�ڵ�![]() �Ķ���Ϊ__________ʱ���ı���
�Ķ���Ϊ__________ʱ���ı���![]() Ϊ�����Σ�
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB��3��BC��4�����Խ���AC�ƶԽ��߽���O��ת���ֱ�AD��BC�ڵ�E��F����P�DZ�DC�ϵ�һ�����㣬�ұ���DP��AE������PE��PF����AE��x��0��x��3����
��1����գ�PC���� ����FC���� �������ú�x�Ĵ���ʽ��ʾ��
��2�����PEF�������Сֵ��
��3�����˶������У�PE��PF�Ƿ�����������������x��ֵ��������������˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com