
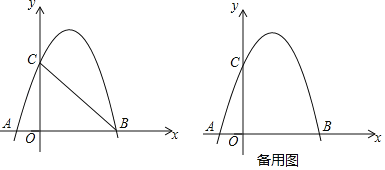
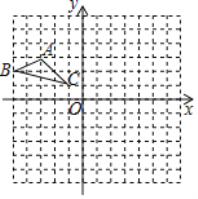
����Ŀ����ͼ��������y��ax2+bx+3��a��0����x�ᣬy��ֱ��ڵ�A����1��0����B��3��0������C���㣮
��1���������ߵĽ���ʽ��
��2��x�����Ƿ���ڵ�P��ʹPC+![]() PB��С�������ڣ��������P�����꼰PC+
PB��С�������ڣ��������P�����꼰PC+![]() PB����Сֵ���������ڣ���˵�����ɣ�
PB����Сֵ���������ڣ���˵�����ɣ�
��3������BC����EΪ�߶�BC�е㣮��M����������һ���㣬����M�Ƶ�E��ת180���õ���N������B��C��M��NΪ������ı����Ǿ���ʱ��ֱ��д����N�����꣮
���𰸡���1��y����x2+2x+3����2��P��![]() ��0����PC+
��0����PC+![]() PB����Сֵ
PB����Сֵ![]() ����3��N��
����3��N��![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��������
��1���Ȱ���������x��Ľ���������������ߵĽ���ʽΪy=a��x+1����x-3����չ�������ɵó����ۣ�
��2����x���·�����ABD=30�㣬��y�Ḻ������D�������OD=![]() ��BD=
��BD=![]() ���������CD=3+
���������CD=3+![]() �����жϳ�����C��P��B��ͬһ��ֱ����ʱ��PC+
�����жϳ�����C��P��B��ͬһ��ֱ����ʱ��PC+![]() ��С����СֵΪCB'�����ɵó����ۣ�
��С����СֵΪCB'�����ɵó����ۣ�
��3�����жϳ���M��x���Ϸ��������ߣ��ٹ������BEM�ס�CFM���ó�![]() ���ɵó����ۣ�
���ɵó����ۣ�
�⣺��1����������y��ax2+bx+3��a��0����x�ύ�ڵ�A����1��0����B��3��0����
���������ߵĽ���ʽΪy��a��x+1����x��3����ax2��2ax��3a��
�ੁ3a��3��
��a����1��
�������ߵĽ���ʽΪy����x2+2x+3��
��2����ͼ��
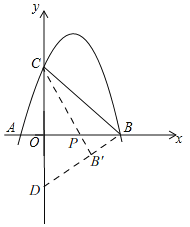
��x���·�����ABD��30������y�Ḻ������D����BD��2OD��
��B��3��0����
��OB��3��
���ݹ��ɶ����ã�BD2��OD2��32��
��4OD2��OD2��9��
��OD��![]() ��BD��
��BD��![]() ��
��
�������ߵĽ���ʽΪy����x2+2x+3��
��C��0��3����
��OC��3��
��CD��3+![]() ��
��
����P��PB'��BD��B'��
��Rt��PB'B��PB'��![]() PB��
PB��
��PC+![]() PB��PC+PB'��
PB��PC+PB'��
����C��P��B��ͬһ��ֱ����ʱ��PC+![]() PB��С����СֵΪCB'��
PB��С����СֵΪCB'��
��S��BCD��![]() CDOB��
CDOB��![]() BDCB'��
BDCB'��
��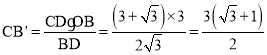
��PC+![]() PB����Сֵ
PB����Сֵ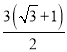 ��
��
��OB��OC��3��
���OBC����OCB��45����
���DBC��45��+30����75����
���BCP��90����75����15����
���OCP��30����
��OC��3��
��OP��![]() ��
��
��P��![]() ��0����
��0����
��3���籸��ͼ��
��M��m����m2+2m+3����
��B��C��M��NΪ������ı����Ǿ��Σ�
���BMC��90����
�ߵ�A��x�Ḻ���ᣬ�ҡ�BOC��90����
���M��x���Ϸ��������ߣ�
����M��ME��x����E����MF��y����F��
���MEO����MFO��90������EOF��
���ı���OEMF�Ǿ��Σ�
���EMF��90����
���BME����CMF��
�� ��BEM����CFM��90����
���BEM�ס�CFM��
��![]()
��![]()
��m��![]() ��
��
��M��![]() ��
��![]() ����
����![]() ��
��![]() ����
����
�ߵ�N�ǵ�M���ڵ�E��![]() ��
��![]() ���ĶԳƵ㣬
���ĶԳƵ㣬
�� ��
��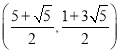



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
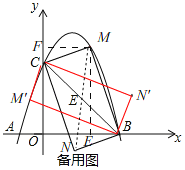
����Ŀ����֪��ABC�ڽ��ڡ�O��AB�ǡ�O��ֱ����OD��AC��AD��OC��
��1����֤���ı���OCAD��ƽ���ı��Σ�
��2����AD���O�������B��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
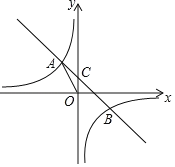
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��ͼ���뷴��������y![]() (kΪ������k��0)��ͼ���ڶ����������ڵ�A��B���㣬��y�ύ��C�㣮��A������Ϊ(m��5)����B������Ϊ(5��n)��tan��AOC
(kΪ������k��0)��ͼ���ڶ����������ڵ�A��B���㣬��y�ύ��C�㣮��A������Ϊ(m��5)����B������Ϊ(5��n)��tan��AOC![]() ��
��
��1����k��ֵ��
��2��ֱ��д����B�����꣬����ֱ��AB�Ľ���ʽ��
��3��P��y����һ�㣬��S��PBC=2S��AOB�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�ڱ߳�Ϊl����������������ͼ��ʾ��
���Ե�CΪλ�����ģ�������ABC��λ��ͼ����A1B1C��ʹ��λ�Ʊ�Ϊ1��2������A1B1Cλ�ڵ�C����࣬����ʾ��A1�����꣮
��������ABC�Ƶ�C˳ʱ����ת90�����ͼ����A2B2C��
���ڢڵ������������B������·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
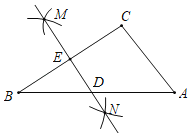
����Ŀ����ͼ������ABC�У������²�����ͼ���ٷֱ��Ե�B�͵�CΪԲ�ģ�����![]() BC�ij�Ϊ�뾶�����������ཻ�ڵ�M��N������ֱ��MN���ֱ�AB��BC�ڵ�D��E������CD������BCA��90����AB��8����CD�ij�Ϊ_____��
BC�ij�Ϊ�뾶�����������ཻ�ڵ�M��N������ֱ��MN���ֱ�AB��BC�ڵ�D��E������CD������BCA��90����AB��8����CD�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��С�������б�¹��£�����˺��������Ҳ�б�����Ϲ�������������У�С����˶��ٶ�v����λ��m/s�����˶�ʱ��t ����λ��s���ĺ���ͼ����ͼ2�����С����˶�·��y����λ��m�����˶�ʱ��t����λ��s��֮��ĺ���ͼ������ǣ� ��
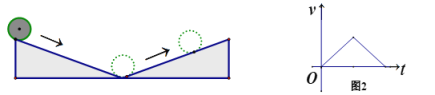
A.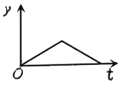 B.
B. C.
C.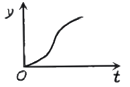 D.
D.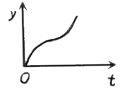
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90��������ABC��ֱ��AB���۵õ���ABD������CD��AB�ڵ�M��E���߶�CM�ϵĵ㣬����BE��F����BDE�����Բ��AD����һ�����㣬����EF��BF��
��1����֤����BEF��ֱ�������Σ�
��2����֤����BEF����BCA��
��3����AB=6��BC=mʱ�����߶�CM�����ڵ�E��ʹ��EF��AB����ƽ�֣���m��ֵ��
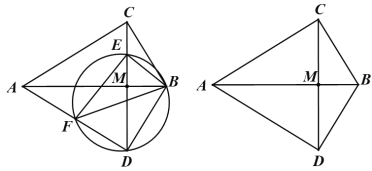
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij������У���֪��ͬС��ļס������ӵ����Ԥѡ���ɼ���ÿ�α����ijɼ�Ϊ0�֣�10�֣�20������������ֱ������в�������ͳ�Ʊ�������ͳ��ͼ��ʾ��
�����Ԥѡ���ɼ�ͳ�Ʊ�
�������� | 1 | 2 | 3 | 4 | 5 |
�ɼ����֣� | 20 | 0 | 20 | x | 20 |
�Ҷ����Ԥѡ���ɼ�����ͳ��ͼ
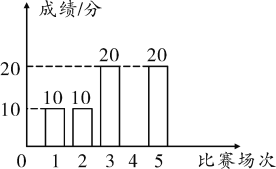
��֪�ס����������Ԥѡ���ɼ���������ͬ��ƽ����Ҳ��ͬ��
��1������ҵ��Ĵ�Ԥѡ���ijɼ���
��2����ӳɼ���ƽ������x��ֵ��
��3���Ӽס�������ǰ3�α����������ѡ��һ�������ijɼ����бȽϣ���ѡ�ļӳɼ������Ҷӳɼ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
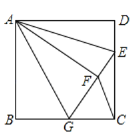
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊa��EΪCD����һ�㣨����˵��غϣ�������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF�����������жϣ��١�EAG��45��������DE��![]() a����AG��CF������EΪCD���е㣬���GFC�����Ϊ
a����AG��CF������EΪCD���е㣬���GFC�����Ϊ![]() a2������CF��FG����
a2������CF��FG����![]() ����BGDE+AFGE��a2��������ȷ����____________����д��������ȷ�жϵ���ţ�
����BGDE+AFGE��a2��������ȷ����____________����д��������ȷ�жϵ���ţ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com