
| A. | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | B. | $\frac{AB}{DE}$=$\frac{BC}{EF}$ | C. | ∠A=∠E | D. | ∠B=∠D |
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题
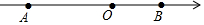 如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.
如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
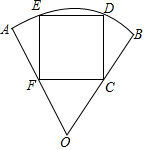 要在半径长为1米、圆心角为60°的扇形铁皮(如图)上截取一块面积尽可能大的正方形,请你设计一个截取方案(画出示意图),并计算这个正方形铁皮的面积(精确到0.01).
要在半径长为1米、圆心角为60°的扇形铁皮(如图)上截取一块面积尽可能大的正方形,请你设计一个截取方案(画出示意图),并计算这个正方形铁皮的面积(精确到0.01).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
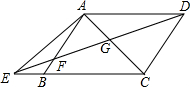 如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且$\frac{FG}{GD}$=$\frac{AD}{CE}$.
如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且$\frac{FG}{GD}$=$\frac{AD}{CE}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
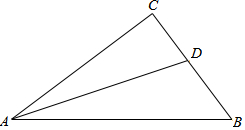 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,AD为△ABC角平分线.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,AD为△ABC角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A,G,H,D且∠1=∠2,∠B=∠C
如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A,G,H,D且∠1=∠2,∠B=∠C查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com