练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
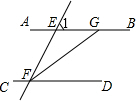
    4．如图，AB∥CD，∠EFG=∠EGF，∠BGF=146°，则∠1的度数为68°．

    分析 由平行线的性质定理可得∴∠1=∠EFD，∠DFG=180°-146°=34°，由三角形内角和定理和补角的定义，可得∠1=∠EFG+∠EGF=2∠EFG，易得$∠DFG=\frac{1}{2}∠1$，可得结果．

    解答 解：∵AB∥CD，
    ∴∠1=∠EFD，
    ∵∠BGF=146°，
    ∠DFG=180°-146°=34°，
    ∵∠EFG+∠EGF+∠FEG=180°，∠1+∠FEG=180°，∠EFG=∠EGF，
    ∴∠1=∠EFG+∠EGF=2∠EFG，
    ∴$∠EFG=\frac{1}{2}∠1$，
    ∴$∠DFG=\frac{1}{2}∠1$，
    ∴∠1=2∠DFG=2×34°=68°．
    故答案为：68°．

    点评 本题主要考查了平行线的性质定理，得出$∠DFG=\frac{1}{2}∠1$是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．计算：
    （1）-$\sqrt{\frac{25}{9}}$
    （2）$\root{3}{0.064}$
    （3）（$\sqrt{5}$+$\sqrt{6}$）-2$\sqrt{6}$
    （4）|2$\sqrt{3}$-3$\sqrt{2}$|-|-3$\sqrt{2}$|

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，在菱形ABCD中，E是AB的中点，且DE⊥AB，AB=10，则∠ABC=120°，对角线AC的长为10$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．若a＞0，且ax=3，ay=2，则ax-2y=$\frac{3}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：
    （1）2$\sqrt{\frac{1}{2}}$-$\sqrt{18}$+$\sqrt{8}$
    （2）（2$\sqrt{3}$-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，EN⊥CD，点M在AB上，∠MEN=156°，当∠BME=66°时，AB∥CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．为了解六年级学生的课外作业情况，某学校从该年级学生中随机抽取了若干名学生，对他们的课外作业时间（单位：min）进行调查，并将收集的数据整理绘制成如下两幅不完整的图表，请根据图中信息，解答下列问题：
     课外作业时间
    （分组）    		 人数
    （频数）
     30～45 5
     45～60 12
     60～75 a
     75～90 10
     90～105 b
    （1）本次调查共抽取了50名学生，a=20，b=3；
    （2）求出作业时间为75～90min的部分对应的扇形圆心角的度数；
    （3）请根据上表绘制频数直方图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

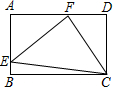    13．如图，E、F分别是矩形ABCD的边AB、AD上的点，∠FEC=∠FCE=45°
    （1）求证：AF=CD；
    （2）若AD=2，△EFC的面积为$\frac{3}{2}$，求线段BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．解方程：$\frac{x-1}{2}=1-\frac{3x+2}{5}$．

    查看答案和解析>>

    同步练习册答案