
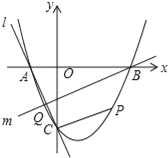
����Ŀ����ͼ��������y=x2+bx+c��x�ύ��A��B���㣬B������Ϊ��3��0������y�ύ�ڵ�C��0����3��
��1���������ߵĽ���ʽ��
��2����P��������λ�ڵ������IJ������˶������ı���ABPC��������ʱ�����P��������ı���ABPC����������
��3��ֱ��l����A��C���㣬��Q��������λ��y�����IJ������˶���ֱ��m������B�͵�Q���Ƿ����ֱ��m��ʹ��ֱ��l��m��x��Χ�ɵ������κ�ֱ��l��m��y��Χ�ɵ����������ƣ������ڣ����ֱ��m�Ľ���ʽ���������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��P������Ϊ��
����2��P��������![]() ��
�� ![]() ��ʱ���ı���ABPC��������������Ϊ
��ʱ���ı���ABPC��������������Ϊ![]() ����3�����ڣ�
����3�����ڣ� ![]() ��
��
�������������������1����B��C��������꣬���ô���ϵ��������������ߵĽ���ʽ��
��2������BC������ABC������Dz���ģ���P��PM��y�ᣬ��BC�ڵ�M�����P�����꣬�ɱ�ʾ��PM�ij�����֪��PMȡ���ֵʱ��PBC�����������ö��κ��������ʿ����P������꼰�ı���ABPC����������
��3����ֱ��m��y�ύ�ڵ�N����ֱ��l�ڵ�G��������AGP=��GNC+��GCN�����Ե���AGB����NGC����ʱ��������AGB=��CGB=90�������֤����AOC�ա�NOB�������ON�ij��������N�����꣬����B��N���ĵ���������ֱ��m�Ľ���ʽ��
���������
��1����B��C����������������߽���ʽ�ɵã� ![]() ����ã�
����ã� ![]() ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2����ͼ1������BC����Py���ƽ���ߣ���BC�ڵ�M����x���ڵ�H��

��![]() �У���y=0�ɵ�
�У���y=0�ɵ�![]() �����x=��1��x=3����A������Ϊ����1��0������AB=3������1��=4����OC=3����S��ABC=
�����x=��1��x=3����A����������1��0������AB=3������1��=4����OC=3����S��ABC=![]() ABOC=
ABOC=![]() ��4��3=6����B��3��0����C��0����3������ֱ��BC����ʽΪy=x��3����P������Ϊ��x��
��4��3=6����B��3��0����C��0����3������ֱ��BC����ʽΪy=x��3����P������Ϊ��x��![]() ������M������Ϊ��x��x��3������P���ڵ����ޣ���PM=
������M������Ϊ��x��x��3������P���ڵ����ޣ���PM=![]() =
=![]() ����S��PBC=
����S��PBC=![]() PMOH+
PMOH+![]() PMHB=
PMHB=![]() PM��OH+HB��=
PM��OH+HB��=![]() PMOB=
PMOB=![]() PM������PM�����ֵʱ����PBC�����������ı���ABPC����������PM=
PM������PM�����ֵʱ����PBC�����������ı���ABPC����������PM=![]() =
=![]() ������x=
������x=![]() ʱ��PMmax=
ʱ��PMmax=![]() ����S��PBC=
����S��PBC=![]() =
=![]() ����ʱP������Ϊ��
����ʱP������Ϊ��![]() ��
�� ![]() ����S�ı���ABPC=S��ABC+S��PBC=6+
����S�ı���ABPC=S��ABC+S��PBC=6+![]() =
=![]() ������P��������
������P��������![]() ��
�� ![]() ��ʱ���ı���ABPC��������������Ϊ
��ʱ���ı���ABPC��������������Ϊ![]() ��
��
��3����ͼ2����ֱ��m��y���ڵ�N����ֱ��l�ڵ�G������AGP=��GNC+��GCN������AGB����NGC����ʱ��������AGB=��CGB������AGB+��CGB=180�������AGB=��CGB=90�������ACO=��OBN����Rt��AON��Rt��NOB�У��ߡ�AOC=��NOB��OC=OB����ACO=��NBO����Rt��AON��Rt��NOB��ASA������ON=OA=1����N������Ϊ��0����1������ֱ��m����ʽΪy=kx+d����B��N�����������ɵ�![]() ����ã�
����ã� ����ֱ��m����ʽΪ
����ֱ��m����ʽΪ![]() ������������������ֱ��m�������ʽΪ
������������������ֱ��m�������ʽΪ![]() ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ����(����)
A. a8��a2=a4 B. a3a2=a6 C. (��2a3)2=4a9 D. 6x23xy=18x3y
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�涨ѧ������ѧѧ�������ɼ�����Ϊ100������ƽʱ�ɼ�ռ50%�����п��Գɼ�ռ20%����ĩ���Գɼ�ռ30%��С�������ɼ����ٷ��ƣ�������86��70��90��С����ѧ�ڵ���ѧѧ�������ɼ��ǣ�������
A. 90B. 86C. 84D. 82
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ֲ������ɳ���������Ŀ��֧�ɣ�ÿ��֧���ֳ�����ͬ��Ŀ��С��֧����С��֧��֧�ɺ����ɵ�����Ŀ��73����ÿ��֧�ɳ�����С��֧����ĿΪ(����)
A. 7 B. 8 C. 9 D. 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������߳�Ϊ�������ܳ�Ϊ11������һ�߳�Ϊ4���������������ı��ǣ�������
A.7
B.6
C.5
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ѧ��ȤС��Ϊ�˽ⱾУѧ���Ե��ӽ�Ŀ��ϲ���������������˲���ѧ����ϲ����һ���Ŀ ���������ѧ��ֻѡһ�ಢ��û�в�ѡ��ģ��������������Ƴ������µ�����ͳ��ͼ�������������������ͼ�����ṩ����Ϣ������������⣺
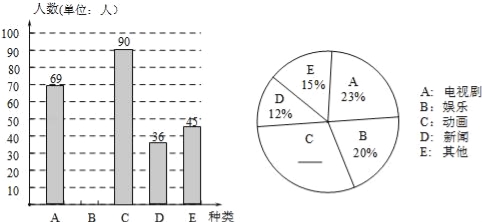
��1���ε����ѧ��������
��2���뽫����ͳ��ͼ������������������Ž�Ŀ������ͳ��ͼ����ռԲ�ĽǵĶ�����
��3��������ѧ��2000��ѧ��������Ƹ�Уϲ�����Ӿ��Ŀ��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com