
分析 (1)根据概率公式求解可得;
(2)画树状图列出所有等可能结果,根据概率公式求解可得.
解答 解:(1)第一次传球后掌声停止,表演节目的有小强、小华、小丽三种情况,
∴小丽即兴表演节目的概率为$\frac{1}{3}$;
(2)设将小明、小强、小华、小丽分别记为A、B、C、D,
画树状图如下: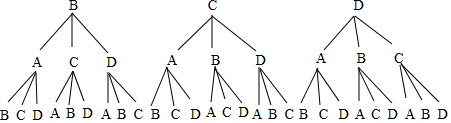
由树状图可知共有27种等可能结果,其中第三次传球后掌声停止时球落在小明手上的有6种结果,
∴小明即兴表演节目的概率为$\frac{6}{27}$=$\frac{2}{9}$.
点评 本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 
| ||||||||||||||||||||||||||||||
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
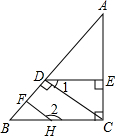 如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空)
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
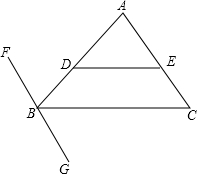 如图,点D、E分别在△ABC的边AB、AC上,且DE∥BC,过点B作直线FG,使∠CBG=∠AED,请判断FG与AC是否平行?并说明理由.
如图,点D、E分别在△ABC的边AB、AC上,且DE∥BC,过点B作直线FG,使∠CBG=∠AED,请判断FG与AC是否平行?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
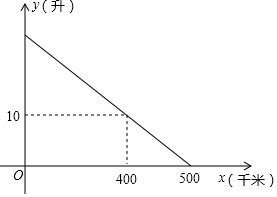 已知某汽车装满油后邮箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶450千米,就应该停车加油.
已知某汽车装满油后邮箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶450千米,就应该停车加油.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A 乙没有抽到自己带来的礼物 | B 乙恰好抽到自己带来的礼物 |
| C 乙抽到一件礼物 | D 只有乙抽到自己带来的礼物 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )
如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )| A. | 8 | B. | 4$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | 8$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com