
某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,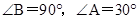 ;图②中,
;图②中, .图③是该同学所做的一个实验:他将△
.图③是该同学所做的一个实验:他将△ 的直角边
的直角边 与△
与△ 的斜边
的斜边 重合在一起,并将△
重合在一起,并将△ 沿
沿 方向移动.在移动过程中,
方向移动.在移动过程中, 两点始终在
两点始终在 边上(移动开始时点
边上(移动开始时点 与点
与点 重合).
重合).
(1) 在△ 沿
沿 方向移动的过程中,该同学发现:
方向移动的过程中,该同学发现: 两点间的距离 ;连接
两点间的距离 ;连接 的度数 .(填“不变”、“ 逐渐变大”或“逐渐变小”)
的度数 .(填“不变”、“ 逐渐变大”或“逐渐变小”)
(2) △ 在移动过程中,
在移动过程中, 与
与 度数之和是否为定值,请加以说明;
度数之和是否为定值,请加以说明;
(3) 能否将△ 移动至某位置,使
移动至某位置,使 的连线与
的连线与 平行?如果能,请求出此时
平行?如果能,请求出此时 的度数,如果不能,请说明理由。
的度数,如果不能,请说明理由。
(1)变小,变大;(2)和为定值,理由见解析;(3)15°.
解析试题分析:(1)利用图形的变化得出F、C两点间的距离变化和,∠FCE的度数变化规律;
(2)利用外角的性质得出∠FEC+∠CFE=∠FED=45°,即可得出答案;
(3)要使FC∥AB,则需∠FCE=∠A=30°,进而得出∠CFE的度数.
试题解析:(1)F、C两点间的距离逐渐变小;连接FC,∠FCE的度数逐渐变大;
(2)∠FCE与∠CFE度数之和为定值;
理由:∵∠D=90°,∠DFE=45°,
又∵∠D+∠DFE+∠FED=180°,
∴∠FED=45°,
∵∠FED是△FEC的外角,
∴∠FEC+∠CFE=∠FED=45°,
即∠FCE与∠CFE度数之和为定值;
(3)要使FC∥AB,则需∠FCE=∠A=30°,
又∵∠CFE+∠FCE=45°,
∴∠CFE=45°-30°=15°.
考点:1.三角形的外角性质;2.平行线的判定;3.三角形内角和定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
【问题提出】如果我们身边没有量角器和三角板,如何作15°大小的角呢?
【实践操作】如图.
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开,得到AD∥EF∥BC.
第二步:再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,得到折痕BM.折痕BM 与折痕EF相交于点P.连接线段BN,PA,得到PA=PB=PN.
【问题解决】
(1)求∠NBC的度数;
(2)通过以上折纸操作,还得到了哪些不同角度的角?请你至少再写出两个(除∠NBC的度数以外).
(3)你能继续折出15°大小的角了吗?说说你是怎么做的.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
完成证明:(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b
证明:∵a⊥c
∴∠1=________
∵b∥c
∴∠1=∠2 ( )
∴∠2=∠1=90°
∴a⊥b ;
(2)如图2:AB∥CD,∠B+∠D=180°,求证:CB∥DE
证明:∵AB∥CD (已知)
∴∠B=________( )
∵∠B+∠D="180°" (已知)
∴∠C+∠D="180°" ( )
∴CB∥DE ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com