
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.例如:由图1可得到![]() .
.

(1)写出由图2所表示的数学等式:________.

(2)写出由图3所表示的数学等式:________.

(3)已知实数![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() .
.
①求![]() 的值.
的值.
②求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①0 ;②1.
;(3)①0 ;②1.
【解析】
(1)根据数据表示出正方形的边长,再根据正方形的面积公式写出等式的左边,再表示出每一小部分的面积,然后根据面积相等即可写出等式;
(2)根据数据表示出阴影正方形的边长,再根据正方形的面积公式写出等式的左边,再用大正方形的面积减去其他八小部分的面积,然后根据面积相等即可写出等式;
(3)①根据(1)的结论变形为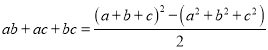 ,代数求值即可得解;
,代数求值即可得解;
②在①的基础上即可求得![]() 的值.
的值.
解:(1)∵大正方形的边长为![]()
∴大正方形的面积可表示为![]()
∵观察图形可知九小部分的面积和为![]()
![]()
∴由图2所表示的数学等式:![]() ;
;
(2)∵阴影正方形的边长为![]()
∴阴影正方形的面积为![]()
∵阴影正方形的面积还以表示为大正方形的面积减去其他八小部分的面积:
![]()
∴由图3所表示的数学等式:![]() ;
;
(3)①∵由图2所表示的数学等式:![]()
∴![]()
∴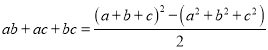
∵![]() ,
,![]()
∴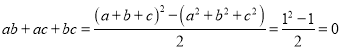 ,即
,即![]() ;
;
②∵![]() ,
,![]()
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.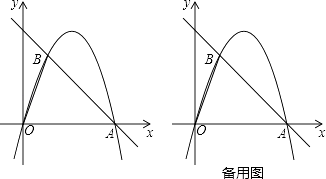
(1)求a,b的值;
(2)点P是线段AB上一动点(点P不与点A、B重合),过点P作PM∥OB交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,设PF的长为t,MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,当S△ACN=S△PMN时,连接ON,点Q在线段BP上,过点Q作QR∥MN交ON于点R,连接MQ、BR,当∠MQR﹣∠BRN=45°时,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(2)求证:无论m取何值,函数y=mx﹣2(m﹣1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为2,求m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
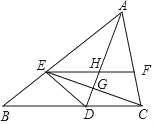
【题目】如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
(1)证明:AD垂直平分CE;
(2)若∠BCE=40°,求∠EHD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
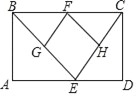
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am﹣b).
其中所有正确的结论是( )
A.①②③
B.①③④
C.①②③⑤
D.①③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com