
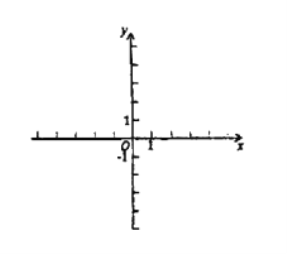
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=1,下列结论:①2a+b=0;②9a+c>3b;③若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2:④若方程ax2+bx+c=﹣3(a≠0)的两根为x1和x2,且x1<x2,则x1<﹣1<3<x2;⑤m(am+b)﹣b<a.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2:④若方程ax2+bx+c=﹣3(a≠0)的两根为x1和x2,且x1<x2,则x1<﹣1<3<x2;⑤m(am+b)﹣b<a.其中正确的结论有( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据对称轴为x=1,再结合对称轴公式即可判断①;当x=﹣3时,y<0,代入即可判断②;找出(![]() ,y3)关于直线x=1的对称点即可判断③;设y=ax2+bx+c,y=﹣3,根据图象可判断④;当x=1时,a+b+c为最大值,可判断⑤.
,y3)关于直线x=1的对称点即可判断③;设y=ax2+bx+c,y=﹣3,根据图象可判断④;当x=1时,a+b+c为最大值,可判断⑤.
解:①由题意可知:对称轴x=1,
∴![]() =1,
=1,
∴2a+b=0,故①正确;
②当x=﹣3时,y<0,
∴y=9a﹣3b+c<0,故②错误;
③(![]() ,y3)关于直线x=1的对称点为(
,y3)关于直线x=1的对称点为(![]() ,y3),
,y3),
由图可知:x<1时,y随着x的增大而减小,
由于﹣3<![]() <
<![]() ,
,
∴y1<y3<y2,故③正确;
④设y=ax2+bx+c,y=﹣3,
由于图象可知:直线y=﹣3与抛物线y=ax2+bx+c有两个交点,
∴方程ax2+bx+c=﹣3(a≠0)的两根为x1和x2,
∴x1<﹣1<3<x2,故④正确;
⑤当x=1时,y=a+b+c,此时a+b+c为最大值,
当x=m时,y=am2+bm+c,
∴am2+bm+c≤a+b+c,
即m(am+b)﹣b≤a,故⑤错误;
故选:C.


科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界上最长的跨海大桥.如图是港珠澳大桥的海豚塔部分效果图,为了测得海豚塔斜拉索顶端A距离海平面的高度,先测出斜拉索底端C到桥塔的距离(CD的长)约为100米,又在C点测得A点的仰角为30°,测得B点的俯角为20°,求斜拉索顶端A点到海平面B点的距离(AB的长).(已知![]() ≈1.732,tan20°≈0.36,结果精确到0.1)
≈1.732,tan20°≈0.36,结果精确到0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
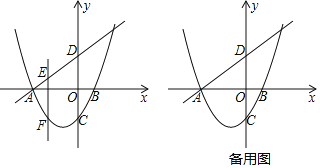
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)交x轴于A,B(1,0)两点,交y轴于点C,一次函数y=x+3的图象交坐标轴于A,D两点,E为直线AD上一点,作EF⊥x轴,交抛物线于点F
(1)求抛物线的解析式;
(2)若点F位于直线AD的下方,请问线段EF是否有最大值?若有,求出最大值并求出点E的坐标;若没有,请说明理由;
(3)在平面直角坐标系内存在点G,使得G,E,D,C为顶点的四边形为菱形,请直接写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点A为中心,把△ABC逆时针旋转120°,得到△AB'C′(点B、C的对应点分别为点B′、C′),连接BB',若AC'∥BB',则∠CAB'的度数为( )

A.45°B.60°C.70°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,n)、B(3,4)是一次函数y1=kx+b的图象与反比例函数![]() 的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线
的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线![]() 和直线y1=kx+b于P、Q两点
和直线y1=kx+b于P、Q两点
(1) 直接写出反比例函数和一次函数的解析式
(2) 当t为何值时,S△BPQ=![]() S△APQ
S△APQ
(3) 以PQ为边在直线PQ的右侧作正方形PQMN,试说明:边QM与双曲线![]() (x>0)始终有交点
(x>0)始终有交点

查看答案和解析>>
科目:初中数学 来源: 题型:
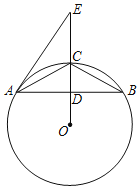
【题目】如图,⊙O为△ABC的外接圆,D为OC与AB的交点,E为线段OC延长线上一点,且∠EAC=∠ABC.
(1)求证:直线AE是⊙O的切线.
(2)若D为AB的中点,CD=6,AB=16
①求⊙O的半径;
②求△ABC的内心到点O的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年“519(我要走)全国徒步日(江夏站)”暨第六届“环江夏”徒步大会5月19日在美丽的花山脚下降重举行.组委会(活动主办方)为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两种纪念品发放.其中甲种纪念品每件售价120元,乙种纪念品每件售价80元.
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品![]() 件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E为BC边上的一点.连结AE.
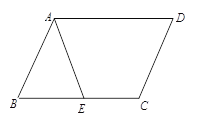
(1)若AB=AE, 求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF︰FA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 和点
和点![]() 给出如下定义:若
给出如下定义:若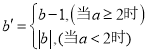 ,则称点
,则称点![]() 为点
为点![]() 的限变点.例如:点
的限变点.例如:点![]() 的限变点的坐标是
的限变点的坐标是![]() 点
点![]() 的限变点的坐标是
的限变点的坐标是![]() 点
点![]() 的限变点的坐标是
的限变点的坐标是![]() .
.
![]() ①点
①点![]() 的限变点的坐标是 ;
的限变点的坐标是 ;
②在点![]() 中有一个点是双曲线
中有一个点是双曲线![]() 上某一个点的限变点,这个点是(填“
上某一个点的限变点,这个点是(填“![]() ”或“
”或“![]() ”)
”)
![]() 若点
若点![]() 在关于
在关于![]() 的二次函数
的二次函数![]() 的图象上,其限变点
的图象上,其限变点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() 或
或![]() 其中
其中![]() .令
.令![]() ,直接写出
,直接写出![]() 的值.
的值.
![]() 若点
若点![]() 在函数
在函数![]() 的图象上,其限变点
的图象上,其限变点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() ,直接写出
,直接写出![]() 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com