
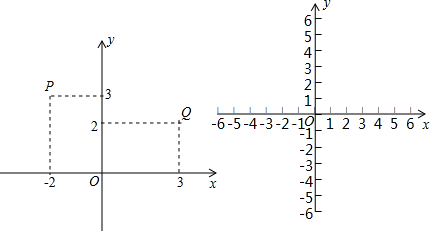
分析 (1)①把各点的横纵坐标的绝对值相加,得4,则是A的同族点;
②因为点B在x轴上,所以设B(x,0),则|x|=4,可得结论;
(2)①首先证明点M的横坐标与纵坐标的绝对值之和为定值3,然后画出图形即可解决问题;
②如图,设P(m,0)为圆心,$\sqrt{2}$为半径的圆与直线y=x-3相切,求出此时P的坐标,即可判断;
解答 解:(1)①∵点A的坐标为(-3,1),
∴3+1=4,
点R(0,4),S(2,2),T(2,-3)中,
0+4=4,2+2=4,2+3=5,
∴点A的同族点的是R,S;
故答案为:R,S;
②∵点B在x轴上,
∴点B的纵坐标为0,
设B(x,0),
则|x|=4,
∴x=±4,
∴B(-4,0)或(4,0);
故答案为:(-4,0)或(4,0);
(2)①由题意,直线y=x-3与x轴交于C(3,0),与y轴交于D(0,-3).
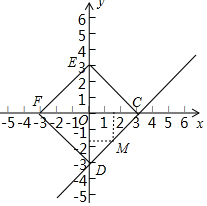
点M在线段CD上,设其坐标为(x,y),
则有:x≥0,y≤0,且y=x-3.
点M到x轴的距离为|y|,点M到y轴的距离为|x|,
则|x|+|y|=x-y=3.
∴点M的同族点N满足横纵坐标的绝对值之和为3.
即点N在右图中所示的正方形CDEF上.
∵点E的坐标为(-3,0),点N在直线x=n上,
∴-3≤n≤3.
②如图,设P(m,0)为圆心,$\sqrt{2}$为半径的圆与直线y=x-3相切,
∵PN=$\sqrt{2}$,∠PCN=∠CPN=45°,
∴PC=2,
∴OP=1,
观察图形可知,当m≥1时,若以(m,0)为圆心,$\sqrt{2}$为半径的圆上存在点N,使得M,N两点为同族点,
再根据对称性可知,m≤-1也满足条件,
∴满足条件的m的范围:m≤-1或m≥1.
点评 本题考查一次函数综合题、同族点的定义、圆的有关知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会利用特殊位置解决数学问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
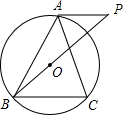 如图,⊙O是△ABC的外接圆,弧AB=弧AC,AP是⊙O的切线,交BO的延长线于点P.
如图,⊙O是△ABC的外接圆,弧AB=弧AC,AP是⊙O的切线,交BO的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
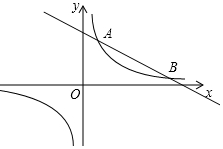 如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
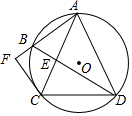 如图,四边形ABCD是⊙O的内接四边形,∠ABD=∠CBD=60°,AC与BD相交于点E,过点C作⊙O的切线,与AB的延长线相交于点F.
如图,四边形ABCD是⊙O的内接四边形,∠ABD=∠CBD=60°,AC与BD相交于点E,过点C作⊙O的切线,与AB的延长线相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 要反映一个家庭每年用于旅游的费用占总支出的百分比宜采用条形统计图 | |
| B. | 打开电视正在播放新闻联播是必然事件 | |
| C. | 方差反映了一组数据的稳定程度 | |
| D. | 检查“天舟一号”飞船各零件的安全性,可采用抽样调查的办法 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com