
����Ŀ��2018������������ǰϦ���˱�ij������1000Ԫ�������ɾջ����ܿ����꣬��������2500Ԫ�����ڶ���
������֪�ڶ����������������ǵ�һ������������2������ÿ�仨�Ľ��۱ȵ�һ���Ľ��۶�![]() Ԫ��
Ԫ��
��1����һ����ÿ���Ľ����Ƕ���Ԫ��
��2������һ���ջ���3Ԫ���ۼ����ۣ�Ҫʹ��������1500Ԫ���������������������ڶ���ÿ��ջ����ۼ������Ƕ���Ԫ��
���𰸡���1��2Ԫ����2���ڶ��������ۼ�����Ϊ![]() Ԫ��
Ԫ��
��������
��1�����һ����ÿ���Ľ�����xԪ����ڶ�����ÿ���Ľ����ǣ�x+0.5��Ԫ����������=�ܼ������۽�ϵڶ����������������ǵ�һ������������2�������ɵó�����x�ķ�ʽ���̣���֮������ɵó����ۣ�
��2���ɵڶ������Ľ��۱ȵ�һ���Ľ��۶�0.5Ԫ������ڶ������Ľ��ۣ���ڶ����ջ����ۼ�ΪmԪ����������=ÿ���������������������������1500Ԫ�����ɵó�����m��һԪһ�β���ʽ����֮���ɵó����ۣ�
��1�����һ����ÿ���Ľ�����xԪ����ڶ�����ÿ���Ľ�����![]() Ԫ��
Ԫ��
��������ã�![]() ��
��
��ã�![]() ��
��
�����飺![]() ��ԭ���̵Ľ⣬�ҷ������⣮
��ԭ���̵Ľ⣬�ҷ������⣮
�𣺵�һ����ÿ���Ľ�����2Ԫ��
��2����![]() ��֪�ڶ����ջ��Ľ���Ϊ
��֪�ڶ����ջ��Ľ���Ϊ![]() Ԫ��
Ԫ��
��ڶ����ջ����ۼ�ΪmԪ��
��������ã�![]() ��
��
��ã�![]() ��
��
�𣺵ڶ��������ۼ�����Ϊ![]() Ԫ��
Ԫ��


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB��30����OPƽ�֡�AOB��PC��OB��OA��C��PD��OB��D�����PC��8����ôPD����____________ ��
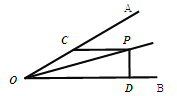
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O���������������ж��ı���ABCDΪƽ���ı��ε��ǣ�������
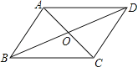
A.AB��CD��AD��BCB.OA��OC��OB��OD
C.AD��BC��AB��CDD.AB��CD��AD��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ����õķֽ���ʽ�������ṫ��ʽ����ʽ���ȣ����еĶ���ʽֻ���������������ֽ⣬��x2��4y2+2x��4y��ϸ�Ĺ۲����ʽ�ӻᷢ�֣�ǰ�������ƽ���ʽ�����������ȡ����ʽ��ǰ�������ֱַ�ֽ���ʽ����������ʽ��Ȼ����ȡ����ʽ�Ϳ����������ʽ�ӵķֽ���ʽ������Ϊ��
x2��4y2+2x��4y
����x2��4y2��+��2x��4y��
����x+2y����x��2y��+2��x��2y��
����x��2y����x+2y+2��
���ַֽ���ʽ�ķ����з���ֽⷨ���������ַ�������������⣺
��1���ֽ���ʽ��x2��6xy+9y2��3x+9y
��2����ABC������a��b��c����a2��b2��ac+bc��0���жϡ�ABC����״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E��AD�ߵ��е㣬![]() ������Ϊ��F������DF�����������ĸ����ۣ�
������Ϊ��F������DF�����������ĸ����ۣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������ȷ�Ľ�����______��
������ȷ�Ľ�����______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����![]() ������������
������������![]() �뷴��������
�뷴��������![]() ��ͼ���ڵ�һ���Ľ��㣬
��ͼ���ڵ�һ���Ľ��㣬![]() �ᣬ����Ϊ��
�ᣬ����Ϊ��![]() ��
��![]() �������2.
�������2.

��1����![]() ��ֵ�Լ������������Ľ���ʽ��
��ֵ�Լ������������Ľ���ʽ��
��2������![]() ��
��![]() ���ϣ���
���ϣ���![]() ����
����![]() Ϊ���ĵ��������Σ����
Ϊ���ĵ��������Σ����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=2![]() ��BC=4����EΪBC����һ���㣬����AE������AEF=��B��EF���ABC����ǡ�ACD��ƽ���߽��ڵ�F����EF��ACʱ��EF�ij�Ϊ_______��
��BC=4����EΪBC����һ���㣬����AE������AEF=��B��EF���ABC����ǡ�ACD��ƽ���߽��ڵ�F����EF��ACʱ��EF�ij�Ϊ_______��
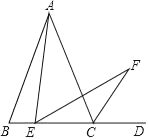
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽����֤����
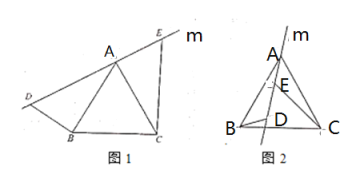
(1)��ͼ1��ֱ��![]() ������������
������������![]() �����
�����![]() ����ֱ��
����ֱ��![]() ��ȡ����
��ȡ����![]() ��
��![]() ��ʹ��
��ʹ��![]() ��
��![]() .ͨ���۲������������߶�
.ͨ���۲������������߶�![]() ��
��![]() ��
��![]() ֮�������������ϵ��������֤����
֮�������������ϵ��������֤����
(2)��(1)�е�ֱ��![]() ���ŵ�
���ŵ�![]() ��ʱ�뷽����תһ���Ƕȵ���ͼ2��λ�ã���ʹ
��ʱ�뷽����תһ���Ƕȵ���ͼ2��λ�ã���ʹ![]() ��
��![]() .ͨ���۲������������߶�
.ͨ���۲������������߶�![]() ��
��![]() ��
��![]() ֮�������������ϵ��������֤��.
֮�������������ϵ��������֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����ǰ��ֱ�Ƕ����غϷ��ã����С�A��30�㣬��CDE��45���������ǰ�ACB��λ�ñ��ֲ����������ǰ�DCE����ֱ�Ƕ���C˳ʱ����תһ�ܣ�����DCE����һ����ABƽ�У����ECB�Ķ���Ϊ____��
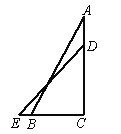
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com