
分析 (1)、(2)利用几何语言作图;
(3)先计算出∠BOC的度数,再分别计算出∠COD和∠BOD的度数,然后画出射线OD;
(4)通过计算∠BOE可判断射线OE是否平分∠BOC.
解答 解:(1)如图,AB和点O为所作;
(2)如图,∠AOC为所作;
(3)能用量角器在∠BOC内部画射线OD,如图;
(4)射线OE不平分∠BOC,
理由如下:∵∠BOE=∠BOD+∠DOE=30°+20°=50°,
而∠BOC=180°-60°120°,
∴射线OE不平分∠BOC,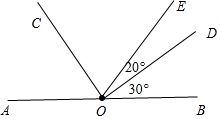
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
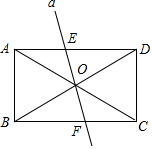 在矩形ABCD中,AC,BD交于点O,直线α经过点O,且α⊥BD交AD于E点,交BC于F点,
在矩形ABCD中,AC,BD交于点O,直线α经过点O,且α⊥BD交AD于E点,交BC于F点,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
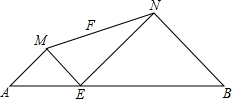 如图,已知AB=9,点E是线段AB上的动点,分别以AE、EB为底边在线段AB的同侧作等腰直角△AME和△BNE,连接MN,设MN的中点为F,当点E从点A运动到点B时,则点F移动路径的长是$\frac{9}{2}$.
如图,已知AB=9,点E是线段AB上的动点,分别以AE、EB为底边在线段AB的同侧作等腰直角△AME和△BNE,连接MN,设MN的中点为F,当点E从点A运动到点B时,则点F移动路径的长是$\frac{9}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
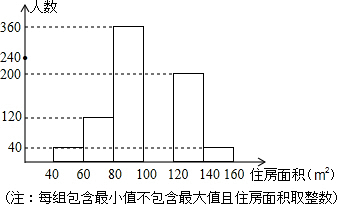 某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机的问卷调查,共发放1000份调查问卷,并全部收回,根据调查问卷,将消费者年收入的情况整理后,制成表格如下,将消费者打算购买住房面积的情况整理后,作出部频数分布直方图如图:
某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机的问卷调查,共发放1000份调查问卷,并全部收回,根据调查问卷,将消费者年收入的情况整理后,制成表格如下,将消费者打算购买住房面积的情况整理后,作出部频数分布直方图如图:| 年收入(万元) | 1.2 | 1.8 | 3.0 | 5.0 | 10.0 |
| 被调查的消费者数(人) | 200 | 300 | 400 | 70 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=0 | B. | x=1 | C. | x=-1 | D. | x=$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
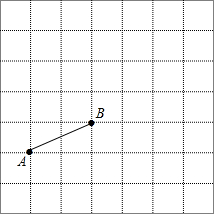 如图,已知A(-1,0),B(1,1),把线段AB平移,使点B落在点D(3,4)处,这时点A移动到点C处.
如图,已知A(-1,0),B(1,1),把线段AB平移,使点B落在点D(3,4)处,这时点A移动到点C处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com