
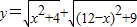 ����Сֵ��Ҫ���������������жϳ�0��x��12���̶����뵽�����Ա߳�Ϊ2+3��12Ϊ�ߵľ��Σ��ҳ�����
����Сֵ��Ҫ���������������жϳ�0��x��12���̶����뵽�����Ա߳�Ϊ2+3��12Ϊ�ߵľ��Σ��ҳ����� ���߶Σ��ٱȽ�
���߶Σ��ٱȽ�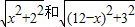 �;��ζԽ��ߵĴ�С��
�;��ζԽ��ߵĴ�С��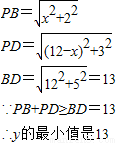
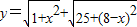 ����Сֵ��
����Сֵ��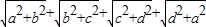 ����Сֵ��
����Сֵ��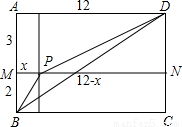
 ��
��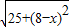 ��ʾ���εĶԽ��߳������ɹ������ABCD��ʹAB=6��AD=8����AB�Ͻ�ȡAM=5��������AMND�����P��MN��һ��MP=x����PN=8-x����������֮���߶���̼���֤�ã�
��ʾ���εĶԽ��߳������ɹ������ABCD��ʹAB=6��AD=8����AB�Ͻ�ȡAM=5��������AMND�����P��MN��һ��MP=x����PN=8-x����������֮���߶���̼���֤�ã�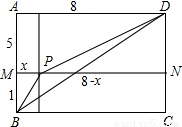 �⣺��1���������ABCD��ʹAB=6��AD=8��
�⣺��1���������ABCD��ʹAB=6��AD=8��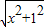 ��
��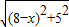
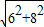 =10
=10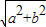 ��EF=
��EF=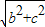 ��FG=
��FG=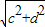 ��DG=
��DG= ��
��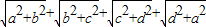 ����Сֵ����BD=
����Сֵ����BD=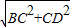 =
=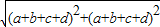 =
=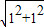 =
=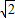 ��
��


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ���ⱳ������֪x��ʵ������y=
���ⱳ������֪x��ʵ������y=| x2+4 |
| (12-x)2+9 |
| x2+22 |
| (12-x)2+32 |
| x2+22 |
| (12-x)2+32 |
|
| 1+x2 |
| 25+(8-x)2 |
| a2+b2 |
| b2+c2 |
| c2+d2 |
| d2+a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���ⱳ������֪x��ʵ������![]() ����Сֵ��Ҫ���������������жϳ�0<x<12,�̶����뵽�����Ա߳�Ϊ2+3��12Ϊ�ߵľ��Σ��ҳ�����
����Сֵ��Ҫ���������������жϳ�0<x<12,�̶����뵽�����Ա߳�Ϊ2+3��12Ϊ�ߵľ��Σ��ҳ�����![]() ���߶Σ��ٱȽ�
���߶Σ��ٱȽ�![]() �;��ζԽ��ߵĴ�С��
�;��ζԽ��ߵĴ�С��
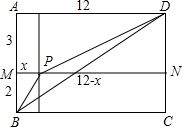
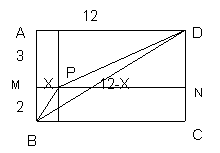 �⣺�������ABCD��ʹAB=5��AD=12.��AB�Ͻ�ȡAM=3��������AMND�����P��MN��һ��MP=x,��PN=12-x,
�⣺�������ABCD��ʹAB=5��AD=12.��AB�Ͻ�ȡAM=3��������AMND�����P��MN��һ��MP=x,��PN=12-x,

��1�� ���ǰ���������ֵ����ķ���������ͼ�������������������![]() ����Сֵ��
����Сֵ��
̽�����£�
��2����֪a,b,c,d����ʵ����a+b+c+d=1����������ͼ����![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com