
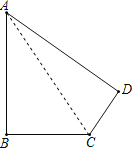
【题目】如图,已知一块四边形的草地ABCD,其中∠B=90°,AB=20m,BC=15m,CD=7m,DA=24m,求这块草地的面积.

【答案】234m2.
【解析】
仔细分析题目,需要求得四边形的面积才能求得结果.连接AC,由AD、CD、AC的长度关系可得△ACD为一直角三角形,AC为斜边;由此看,四边形ABCD由Rt△ACD和Rt△ABC构成,则容易求解.
解:如图,连接AC,如图所示.
∵∠B=90°,AB=20m,BC=15m,
∴AC=![]() =
=![]() =25m.
=25m.
∵AC=25m,CD=7m,AD=24m,
∴AD2+DC2=AC2,
∴△ACD是直角三角形,且∠ADC=90°,
∴S△ABC=![]() ×AB×BC=
×AB×BC=![]() ×20×15=150m2,S△ACD=
×20×15=150m2,S△ACD=![]() ×CD×AD=
×CD×AD=![]() ×7×24=84m2,
×7×24=84m2,
∴S四边形ABCD=S△ABC+S△ACD=234m2.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面内,两条直线L1,L2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线L1,L2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有_____个

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陆老师去水果批发市场采购苹果,他看中了A,B两家苹果,这两家苹果品质一样,零售价都我6元/千克,批发价各不相同.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
数量范围(千克) | 0~500部分 | 500以上~1500 | 1500以上~2500部分 | 2500以上部分 |
价格补贴 | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发700千克苹果,则他在A、B两家批发分别需要多少元?
(2)如果他批发x千克苹果(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)A、B两店在互相竞争中开始了互怼,B说A店的苹果总价有不合理的,有时候买的少反而贵,忽悠消费者;A说B的总价计算太麻烦,把消费者都弄糊涂了;旁边陆老师听完,提出两个问题希望同学们帮忙解决:
问题1:能否举例说明A店买的多反而便宜?
问题2:B店老板比较聪明,在平时工作中发现有巧妙的方法:总价=购买数量×单价+价格补贴;
注:不同的单价,补贴价格也不同;只需提前算好即可填下表:
数量范围(千克) | 0~500部分 | 500以上~1500 | 1500以上~2500 | 2500以上部分 |
价格补贴 | 0元 | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一串图形按如图所示的规律排列.

(说明:下列所指的小正方形都是与第1个图形一样大小的正方形)
(1)第5个图形中有几个小正方形?第6个图形呢?
(2)求出第![]() 个图形中小正方形的个数.
个图形中小正方形的个数.
(3)求出第20个图形中小正方形的个数.
(4)是否存在某个图形,其小正方形的个数恰好是下列各数:① 5050;②1000.给出你的判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
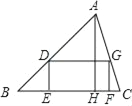
【题目】如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.
(1)求证:AMBC=AHDG;
(2)加工成的矩形零件DEFG的面积能否等于25cm2?若能,求出宽DE的长度;否则,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第10个图中共有点的个数是 ( )
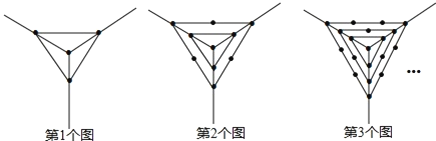
A.109个B.136个C.166个D.199个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=120°,以AC、BC为边向外作等边△ACF和等边△BCF,点P、M、N分别为AB、CF、CE的中点
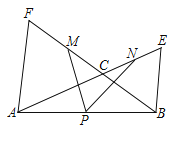
(1) 求证:PM=PN
(2) 求证:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
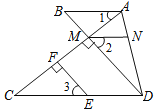
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个正整数m,如果m=k(k+1),其中k是正整数,则称m为“矩数”,k 为m的最佳拆分点.例如,56=7×(7+1),则56是一个“矩数”,7为56的最佳拆分点.
(1)求证:若“矩数”m是3的倍数,则m一定是6的倍数;
(2)把“矩数”p与“矩数”q的差记为 D(p,q),其中p>q,D(p,q)>0.例如,20=4×5,6=2×3,则 D(20,6)=20﹣6=14.若“矩数”p的最佳拆分点为t,“矩数”q的最佳拆分点为s,当 D(p,q)=30时,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com