
 如图,某旅游景点的入口是一抛物线形拱门,它在地面上的水平宽度为10米,两侧距离地面4米高处各有一挂横匾用的铁环,两铁环间的水平距离为6米,则该拱门最高处到地面的距离为$\frac{25}{4}$米.
如图,某旅游景点的入口是一抛物线形拱门,它在地面上的水平宽度为10米,两侧距离地面4米高处各有一挂横匾用的铁环,两铁环间的水平距离为6米,则该拱门最高处到地面的距离为$\frac{25}{4}$米. 分析 由题意可知,以地面为x轴,大门左边与地面的交点为原点建立平面直角坐标系,抛物线过(0,0)、(10,0)、(2、4)、(8、4),运用待定系数法求出解析式后,求函数值的最大值即可.
解答 解:以地面为x轴,大门左边与地面的交点为原点建立平面直角坐标系,
则抛物线过O(0,0)、E(10,0)、A(2、4)、B(8、4)四点,
设该抛物线解析式为:y=ax2+bx+c,
则$\left\{\begin{array}{l}{c=0}\\{100a+10b+c=0}\\{4a+2b+c=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{5}{2}}\\{c=0}\end{array}\right.$.
故函数解析式为:y=-$\frac{1}{4}$x2+$\frac{5}{2}$x.
当x=5时,可得y=-$\frac{25}{4}$+$\frac{25}{2}$=$\frac{25}{4}$米.
故答案为:$\frac{25}{4}$.
点评 本题考查了坐标的求法及二次函数的实际应用,关键是建立数学模型,借助二次函数解决实际问题,注意根据线段长度得出各点的坐标,难度一般.


科目:初中数学 来源: 题型:选择题
| A. | a2×a3=a6 | B. | 2$\sqrt{3}×\sqrt{3}÷\sqrt{3}=2\sqrt{3}$ | C. | x2-5x+6=(x-6)(x+1) | D. | a2+a3=a5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?
如图,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
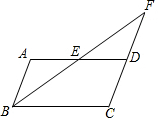 如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则S△EDF与S△BCF的比值是( )
如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则S△EDF与S△BCF的比值是( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $2{x^2}-\frac{3}{x}=1$ | B. | x2=0 | C. | (2x+1)(2x-1)=4x(x+7) | D. | x(x2-5)=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
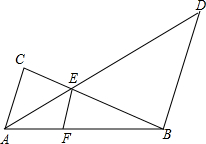 如图,AC∥BD,AD和BC相交于点E,EF∥AC交AB于点F,且AE=p,BD=q,EF=r.
如图,AC∥BD,AD和BC相交于点E,EF∥AC交AB于点F,且AE=p,BD=q,EF=r.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com