Question

已知抛物线y=x²-（2m-1）x+4m-6．
（1）试说明对于每一个实数m，抛物线都经过x轴上的一个定点A；
（2）设抛物线与x轴的另一个交点为B（A、B不重合），顶点为C，若△ABC为直角三角形，试求m的值；
（3）在满足（2）的条件时，若点B在点A的左侧，试问：抛物线上是否存在点D，使得以A、B、C、D为顶点的四边形是梯形？若存在，求出D点坐标；若不存在，说明理由．

Answer 1

分析：（1）令x²-（2m-1）x+4m-6=0，利用求根公式可解得：x₁=2m-3，x₂=2，所以对于每一个实数m，抛物线都经过x轴上的一个定点A（2，0）．
（2）根据抛物线的对称性且△ABC为直角三角形，可得△ABC为等腰直角三角形且∠ACB=90°，过点C作CP⊥AB于P，则CP=

1

2

AB，利用抛物线y=x²-（2m-1）x+4m-6的顶点公式可知，顶点为C(

2m-1

2

，

20m-4m2-25

4

)，可得4m²-20m+25=10-4m，解得m1=

3

2

，m2=

5

2

（舍去）或4m²-20m+25=4m-10，m3=

7

2

，m4=

5

2

（舍去），综合可得：m的值为

3

2

或

7

2

．
（3）先求得抛物线方程为y=x²-2x，设存在点D，使得以A、B、C、D为顶点的四边形是梯形，
i）若BD∥AC，设直线AC方程为y=k₁x+b₁，把A、C坐标代入直线方程得，直线AC方程为y=x-2，直线BD方程为y=x，联立方程组可求得交点坐标为D（3，3）．
ii）若AD∥BC，由于直线BC方程为y=-x，所以，可设直线AD的方程为y=-x+b₂，把A（-2，0）代入得，y=-x+2，联立方程组可求得交点坐标为D（-1，3）．
所以抛物线上存在点D（3，3）或D（-1，3），使得以为A、B、C、D为顶点的四边形是梯形．

解答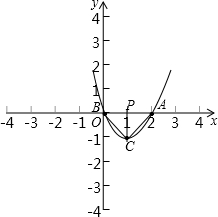：解：（1）令x²-（2m-1）x+4m-6=0，
有求根公式解得：x₁=2m-3，x₂=2
∴对于每一个实数m，抛物线都经过x轴上的一个定点A（2，0）；

（2）根据抛物线的对称性且△ABC为直角三角形，可得△ABC为等腰直角三角形且∠ACB=90°如图，
过点C作CP⊥AB于P，则CP=

1

2

AB，
∵抛物线y=x²-（2m-1）x+4m-6的顶点
为C(

2m-1

2

，

20m-4m2-25

4

)
∴CP=|

20m-4m2-25

4

|，

1

2

AB=

1

2

|(2m-3)-2|=|

2m-5

2

||

20m-4m2-25

4

|=|

2m-5

2

|
∴4m²-20m+25=10-4mm1=

3

2

，m2=

5

2

（舍去）
或4m²-20m+25=4m-10m3=

7

2

，m4=

5

2

（舍去）
综上可得：m的值为

3

2

或

7

2

（3）依题意得：m=1.5，此时抛物线方程为y=x²-2x
设存在点D，使得以A、B、C、D为顶点的四边形是梯形，
i）若BD∥AC，设直线AC方程为y=k₁x+b₁，
把A、C坐标代入直线方程得，

0=2k1+b1 -1=k1+b1

解得

k1=1 b1=-2

∴直线AC方程为y=x-2
∴直线BD方程为y=x
由

y=x y=x2-2x

得

x1=0 y1=0

x2=3 y2=3

∴D（3，3）
ii）若AD∥BC，由于直线BC方程为y=-x，
所以，可设直线AD的方程为y=-x+b₂，
把A（-2，0）代入得，0=-2+b₂，
∴b₂=2，∴y=-x+2．
∴

y=-x+2 y=x2-2x

解得

x1=2 y1=0

x2=-1 y2=3

．
∴D（-1，3）
综上可得：抛物线上存在点D（3，3）或D（-1，3），使得以为A、B、C、D为顶点的四边形是梯形．

点评：本题考查二次函数的综合应用，其中涉及到的知识点有待定系数法求函数解析式和梯形的性质，函数图象交点的意义等．要熟练掌握才能灵活运用．