
【题目】如图,在平面直角坐标系中,△ABC与△A1B1C1 , 关于点E成中心对称.
(1)画出对称中心E,并写出点E的坐标是 ;
(2)P(a,b)是边上的一点,△ABC经过平移后点P的对应点为P2(a+6,b+2),请画出上述平移后的△A2B2C2 . 并写出点A2坐标为 ,点B2坐标为 ;
(3)直接判断并写出△A1B1C1 , 与△A2B2C2的位置关系为 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A,C在反比例函数y= ![]() (a>0)的图像上,点B,D在反比例函数y=
(a>0)的图像上,点B,D在反比例函数y= ![]() (b<0)的图像上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=5,CD=4,AB与CD的距离为6,则a﹣b的值是 .
(b<0)的图像上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=5,CD=4,AB与CD的距离为6,则a﹣b的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离为|4﹣1|= ;表示5和﹣2两点之间的距离为|5﹣(﹣2)|=|5+2|= ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|,如果表示数a和﹣2的两点之间的距离是3,那么a= .
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a= 时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值为 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,AB=AC,∠BAC=∠EPF=90°,点P是BC的中点,两边PE、PF分别交AB,AC于E、F,连接EF、AP.有下列结论①AE=CF ②EF=AP ③△EPF是等腰直角三角形④![]() ,其中正确的有( )个
,其中正确的有( )个

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一段15m长的旧围墙AB,现打算利用该围墙的一部分(或全部)为一边,再用32m长的篱笆围成一块长方形场地CDEF.
(1)怎样围成一个面积为126m2的长方形场地?
(2)长方形场地面积能达到130m2吗?如果能,请给出设计方案,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的单位长度为1,A、B两点表示的数是互为相反数;
(1)点A表示的数是 ,点B表示的数是
(2)数轴上一个动点P先向左移动2个单位长度,再向右移动5个单位到达点M,若点M表示的数是1,则点P所表示的数是
(3)(背景知识)数轴上,点A、B表示的数分别记为a、b,当点P在A、B之间,且到A、B的距离相等,即PA=PB,则点P表示的数可记为![]() .
.
若点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度向右运动,点P以1个单位长度/秒的速度从O点向右运动.当三点同时运动时,不妨设运动时间为t秒,(t>0)
①点P表示的数为 ;点A表示的数为 ;点B表示的数为 .(用含t的式子表示)
②当t为何值时,点A、点B、点P三点之间恰好有一个点到其他两个点的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习有理数的乘法后,老师给同学们这样一道题目:计算:49![]() ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下:
小明:原式=﹣![]() ×5=﹣
×5=﹣![]() =﹣249
=﹣249![]() ;
;
小军:原式=(49+![]() )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+![]() ×(﹣5)=﹣249
×(﹣5)=﹣249![]() ;
;
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19![]() ×(﹣8)
×(﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=4m,∠A=30°,则DE等于( )
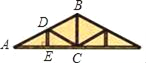
A. 1m B. 2m C. 3m D. 4m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com