
| x(元) | 180 | 200 | 220 | … |
| y (件) | 850 | 750 | 650 | … |
分析 (1)根据题意和表格中的数据可以求得月销售量y(件)与销售价x(元)的函数关系式;
(2)根据(1)中的函数关系式,将x=240代入求得销售量,然后根据利润=(售价-进价)×销售量,即可解答本题.
解答 解:(1)设此一次函数解析式为y=kx+b,
$\left\{\begin{array}{l}{180k+b=850}\\{200k+b=750}\end{array}\right.$,得$\left\{\begin{array}{l}{k=-5}\\{b=1750}\end{array}\right.$,
∴y=-5x+1750,
答:月销售量y(件)与销售价x(元)的函数关系式为y=-5x+1750;
(2)当销售价定为240元时,
则每月的销售量为:y=-5×240+1750=550(件),
所获销售利润为:(240-150)×550=49500(元),
答:销售价定为240元时,每月的销售利润是49500元.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质解答.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知平行四边形ABCD的对角线AC与BD相交于点O,过点O作EF⊥BD,与边AD、BC分别交于点E、F.求证:四边形BEDF是菱形.
如图,已知平行四边形ABCD的对角线AC与BD相交于点O,过点O作EF⊥BD,与边AD、BC分别交于点E、F.求证:四边形BEDF是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
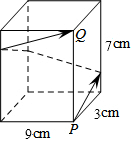 如图,长方体的底面边长分别为9cm和3cm,高为7cm,若一只蚂蚁从P开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为25cm.
如图,长方体的底面边长分别为9cm和3cm,高为7cm,若一只蚂蚁从P开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为25cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com