
【题目】第五届中国机器人峰会将于5月9日在余姚开幕,某公司购买一种T恤衫参加此次峰会.了解到某商店正好有这种T恤衫的促销,当购买10件时每件140元,购买数量每增加1件单价减少1元;当购买数量为60件(含60件)以上时,一律每件80元.
(1)如果购买![]() 件(10<
件(10<![]() <60),每件的单价为
<60),每件的单价为![]() 元,请写出
元,请写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果该公司共购买了100件T恤衫,由于某种原因需分两批购买,且第一批购买量多于30件且少于60件.已知购买两批T恤衫一共花了9200元,求第一批T恤衫的购买数量.
【答案】(1)y=150-x;(2)40件
【解析】分析:(1)若购买x件(10<x<60),每件的单价=140-(购买数量-10),依此可得y关于x的函数关系式;
(2)设第一批购买x件,则第二批购买(100-x)件,分两种情况:①当30<x≤40时,则60≤100-x<100;②当40<x<60时,则40<100-x<60;根据购买两批T恤衫一共花了9200元列出方程求解即可.
详解:(1)购买x件(10<x<60)时,y=140-(x-10)=150-x.
故y关于x的函数关系式是y=150-x.
(2)设第一批购买x件,则第二批购买(100-x)件.
①当30<x≤40时,则60≤100-x<100,则x(150-x)+80(100-x)=9200,
解得![]() =30(舍去),
=30(舍去),![]() =40;
=40;
②当40<x<60时,则40<100-x<60,
则x(150-x)+(100-x) [150-(100-x)]=9200,
解得x=30或x=70,但40<x<60,所以无解;
答:第一批购买数量为40件.


科目:初中数学 来源: 题型:
【题目】符号“f”表示一种运算,它对一些数的运算如下:f(1)=1+![]() ,f(2)=1+
,f(2)=1+![]() ,f(3)=1+
,f(3)=1+![]() ,f(4)=1+
,f(4)=1+![]() …
…
(1)利用以上运算规律,写出f(2017)=__________;
(2)计算:f(1)f(2)f(3)…f(100)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数),并且重复运算,如取n=26,则
为奇数的正整数),并且重复运算,如取n=26,则![]()
则当n=898时,第2018次“F”运算的结果是( )
A. 8 B. 6 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线l1:y=![]() (x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
(x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
A.y=![]() (x﹣2)2+4
(x﹣2)2+4
B.y=![]() (x﹣2)2+3
(x﹣2)2+3
C.y=![]() (x﹣2)2+2
(x﹣2)2+2
D.y=![]() (x﹣2)2+1
(x﹣2)2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC折叠,使B落在E处,AE交CD于点F,则下列结论中不一定成立的是( )
A.AD=CE
B.AF=CF
C.△ADF≌△CEF
D.∠DAF=∠CAF
查看答案和解析>>
科目:初中数学 来源: 题型:
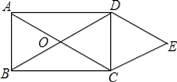
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形.
(2)若AB=6,BC=8,求四边形OCED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
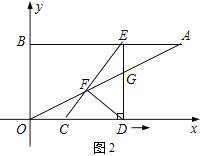
【题目】如图1,已知点A(8,4),点B(0,4),线段CD的长为3,点C与原点O重合,点D在x轴正半轴上.线段CD沿x轴正方向以每秒1个单位长度的速度向右平移,过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F(如图2),设运动时间为t.当E点与A点重合时停止运动.
(1)求线段CE的长;
(2)记△CDE与△ABO公共部分的面积为S,求S关于t的函数关系式;
(3)如图2,连接DF.
①当t取何值时,以C、F、D为顶点的三角形为等腰三角形?
②△CDF的外接圆能否与OA相切?如果能,直接写出此时t的值;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离为|4﹣1|= ;表示5和﹣2两点之间的距离为|5﹣(﹣2)|=|5+2|= ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|,如果表示数a和﹣2的两点之间的距离是3,那么a= .
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a= 时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值为 .
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com