
 正方形ABCD中,点P为边AD上的一点,DE⊥CP于E,延长CP到F,使得CE=EF,连接DF、AF,过点D作∠ADF的角平分线,交CF于H,连结BH.
正方形ABCD中,点P为边AD上的一点,DE⊥CP于E,延长CP到F,使得CE=EF,连接DF、AF,过点D作∠ADF的角平分线,交CF于H,连结BH.分析 (1)作辅助线,构建全等三角形,证明△FDH≌△CDK,得DH=DK,则△HDK是等腰直角三角形,由DE⊥FC,根据等腰三角形三线合一得:HE=EK,利用直角三角形斜边中线等于斜边一半得出结论;
(2)作辅助线,构建四边形NBMH,证明四边形NBMH是正方形,得∠NBM=90°,再证明△FHD≌△AHD,得∠HAD=∠HFD,FH=AH,则△AHF是等腰直角三角形,根据性质∠FAH=45°,由矩形NBMH是正方形,根据正方形的一条对角线平分一组对角:HB平分∠NHM,得∠AHB=$\frac{1}{2}$∠NHM=45°,所以∠FAH=∠AHB=45°,则BH∥AF.
解答 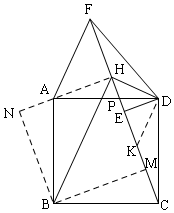 证明:(1)过D作DK⊥DH,交PC于K,
证明:(1)过D作DK⊥DH,交PC于K,
∴∠HDK=∠ADC=90°,
∴∠HDA+∠ADK=∠ADK+∠CDK,
∴∠HDA=∠CDK,
∵DE⊥FC,EF=EC,
∴DF=DC=AD,
∴∠DFH=∠DCK,
∵DH平分∠ADF,
∴∠HDA=∠HDF,
∴∠HDF=∠CDK,
∴△FDH≌△CDK,
∴DH=DK,
∵DE⊥FC,
∴HE=EK,
∴DE=$\frac{1}{2}$HK=HE;
(2)连接HA并延长,过B作BN⊥AH,交HA的延长线于N,过B作BM⊥FC于M,
∵AD=DF,∠HDF=∠HDA,DH=DH,
∴△FHD≌△AHD,
∴∠HAD=∠HFD,FH=AH,
∴∠HAD=∠FCD,
∴∠AHC=∠ADC=90°,
∴△AHF是等腰直角三角形,
∴∠FAH=45°,
∵∠BNH=∠BMH=90°,
∴四边形NBMH是矩形,
∴∠NBM=∠ABC=90°,
∴∠NBA=∠MBC,
∵AB=BC,∠ANB=∠BMC=90°,
∴△ANB≌△CMB,
∴BN=BM,
∴矩形NBMH是正方形,
∴HB平分∠NHM,
∴∠AHB=$\frac{1}{2}$∠NHM=45°,
∴∠FAH=∠AHB=45°,
∴BH∥AF.
点评 本题考查了正方形的性质、等腰三角形三线合一的性质、等腰直角三角形和三角形全等的性质和判定,本题的关键是辅助线的作法,有难度,通过作垂线得到全等三角形和四边形NBMH,从而使问题得以解决.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
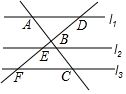 如图,已知l1∥l2∥l3,直线AC、DF分别交直线l1、l2、l3于点A、B、C,和点D、E、F,若DE=2,DF=3,则下列结论中,错误的是( )
如图,已知l1∥l2∥l3,直线AC、DF分别交直线l1、l2、l3于点A、B、C,和点D、E、F,若DE=2,DF=3,则下列结论中,错误的是( )| A. | $\frac{AD}{CF}$=$\frac{2}{3}$ | B. | $\frac{BC}{AB}$=$\frac{1}{2}$ | C. | $\frac{AB}{AC}$=$\frac{2}{3}$ | D. | $\frac{EF}{DF}$=$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
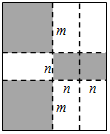 如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com