
分析 分类讨论点C在AB上,点C在AB的延长线上,根据线段的中点,三等分点的性质,可得BM、BN的长,根据线段的和差,可得答案.
解答 解:(1)点C在射线AB上,如:,
点M是线段AB的中点,点N是线段BC的三等分点,
MB=$\frac{1}{2}$AB=3,BN=$\frac{1}{3}$CB=4,或BN=$\frac{2}{3}$BC=8,
MN=BM+BN=3+4=7,或MN=BM+BN=3+8=11;
(2)点C在射线BA上,如: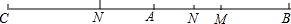
点M是线段AB的中点,点N是线段BC三等分点,
MB=$\frac{1}{2}$AB=3,BN=$\frac{1}{3}$CB=4,或BN=$\frac{2}{3}$BC=8,
MN=BN-BM=4-3=1,或MN=BN-BM=8-3=5.
点评 本题考查了两点间的距离,分类讨论是解题关键,根据线段中点的性质,线段的和差,可得出答案.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
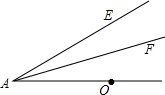 如图,AF平分∠OAE,M是射线AF上一动点,N是线段AO上一动点,判断是否存在点M、N.使得OM+NM的值最小?若存在,请画出M、N点,并加以说明:若不存在,请说明理由.
如图,AF平分∠OAE,M是射线AF上一动点,N是线段AO上一动点,判断是否存在点M、N.使得OM+NM的值最小?若存在,请画出M、N点,并加以说明:若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 二次函数y=x2+bx的图象如图,对称轴为x=-2.若关于x的一元二次方程x2+bx-t=0(t为实数)在-5<x<2的范围内有解,则t的取值范围是-4≤t<12.
二次函数y=x2+bx的图象如图,对称轴为x=-2.若关于x的一元二次方程x2+bx-t=0(t为实数)在-5<x<2的范围内有解,则t的取值范围是-4≤t<12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O的半径为5cm,AB、AC是⊙O的两条弦,AB=6$\sqrt{2}$cm,AC=8cm.过点O作一个圆与AC相切,则这个圆的半径是多少?它与AB具有怎样的位置关系?为什么?
如图,⊙O的半径为5cm,AB、AC是⊙O的两条弦,AB=6$\sqrt{2}$cm,AC=8cm.过点O作一个圆与AC相切,则这个圆的半径是多少?它与AB具有怎样的位置关系?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
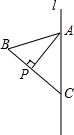 如图,已知△ABC点AC在直线l上,∠B=60°,∠ACB=50°,AP⊥BC,垂足为P.
如图,已知△ABC点AC在直线l上,∠B=60°,∠ACB=50°,AP⊥BC,垂足为P.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于H,且HD=DC,那么下列结论中正确的是( )
如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于H,且HD=DC,那么下列结论中正确的是( )| A. | △ADC≌△BDH | B. | HE=EC | C. | AH=BD | D. | △AHE≌△BHD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com