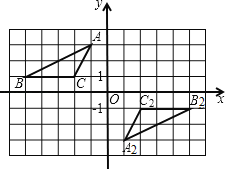
[题目]如图.在平面直角坐标系中.A(﹣1.3).B(﹣5.1).C(﹣2.1).(1)△ABC的面积为 .(2)在图中作出△ABC关于x轴的对称图形△A1B1C1.并写出点A1的坐标.(3)请说明△A2B2C2是由△A1B1C1经过怎样的变换得到的? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在平面直角坐标系中，A(﹣1，3)、B(﹣5，1)、C(﹣2，1).

(1)△ABC的面积为______.

(2)在图中作出△ABC关于x轴的对称图形△A1B1C1，并写出点A1的坐标.

(3)请说明△A2B2C2是由△A1B1C1经过怎样的变换得到的？

【答案】(1)3；(2)画图见解析；点A1的坐标为(﹣1，﹣3)；(3)△A2B2C2是由△A1B1C1经过关于y轴对称得到.

【解析】

(1)利用三角形面积公式计算；

(2)利用关于x轴对称的点的坐标特征写出A1、B1、C1的坐标，然后描点即可；

(3)利用关于y轴对称的点的坐标特征进行判断.

解：(1)S△ABC＝×3×2＝3；

故答案为3；

(2)如图，△A1B1C1为所作；点A1的坐标为(﹣1，﹣3)；

(3)△A2B2C2是由△A1B1C1经过关于y轴对称得到.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】在一个箱子里放有个白球和个红球，它们除颜色外其余都相同．

判断下列甲乙两人的说法，认为对的在后面括号内答“√”，错的打“”．

甲：“从箱子里摸出一个球是白球或者红球”这一事件是必然事件________；

乙：从箱子里摸出一个球，记下颜色后放回，搅匀，这样连续操作三次，其中必有一次摸到的是白球________；

小明说：从箱子里摸出一个球，不放回，再摸出一个球，则“摸出的球中有白球”这一事件的概率为，你认同吗？请画树状图或列表计算说明．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知，在△ABC中，∠A=90°，AB=AC，点D为BC的中点．

（1）如图①，若点E、F分别为AB、AC上的点，且DE⊥DF，求证：BE=AF；

（2）若点E、F分别为AB、CA延长线上的点，且DE⊥DF，那么BE=AF吗？请利用图②说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，点是线段的中点，过点的射线与成的角，点为射线上一动点，给出以下四个结论：

①当，垂足为时，；

②当时，；

③在射线上，使为直角三角形的点只有1个；

④在射线上，使为等腰三角形的点只有1个；

其中正确结论的序号是___．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知，，，、、在同一直线上，则的度数为__________.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知△ABC是等边三角形.

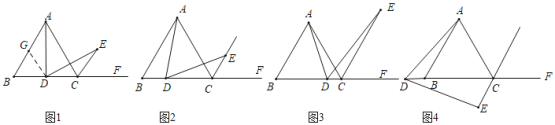
(1)如图1，点D是边BC的中点，∠ADE＝60°，且DE交△ABC外角∠ACF的平分线CE于点E，求证：AD＝DE；(提示：取AB的中点G，连接DG)

(2)小颖对(1)题进行了探索：如果将(1)题中的“点D是边BC的中点”改为“点D是直线BC上任意一点(B、C两点除外)”，其它条件不变，结论AD＝DE是否仍然成立？小颖将点D的位置分为三种情形，画出了图2、图3、图4，现在请你在图2、图3、图4中选择一种情形，帮小颖验证：结论AD＝DE是否仍然成立？