
 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:单选题
同时抛掷A,B两个均匀的小正方体(每个面上分别标有数字1、2、3、4、5、6),设两个正方体朝上的数字分别是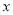 ,
,  ,并 以此确定点
,并 以此确定点 ,那么点P落在抛物线
,那么点P落在抛物线 上的概率是( )
上的概率是( )
A.  B.
B. 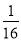 C.
C. 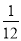 D.
D. 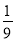
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
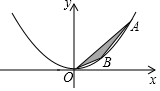 问题情景:
问题情景:| mn | m-n | S | |
| m=3,n=1 | 3 | 2 | 3 |
| m=5,n=2 | 10 | 3 | 15 |
| 2mn | m-n | S | |
| m=3,n=1 | 6 | 2 | 6 |
| m=5,n=2 | 20 | 3 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线AB、CD、EF相交于点O.
如图,直线AB、CD、EF相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
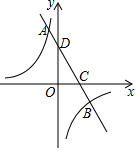 已知直线y=mx+4与反比例函数y=$\frac{k}{x}$(k<0)的图象交于A,B两点,与x轴,y轴分别交于点C,D,OD=2OC,点A的纵坐标为6.
已知直线y=mx+4与反比例函数y=$\frac{k}{x}$(k<0)的图象交于A,B两点,与x轴,y轴分别交于点C,D,OD=2OC,点A的纵坐标为6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com