
分析 (1)原式配方变形后,利用非负数的性质列出不等式,求出不等式的解集即可确定出m的范围;
(2)先由已知条件变形得到x2-x=1,再利用整体代入思想计算即可.
解答 解:(1)配方得:原式=${({x+\frac{1}{2}})^2}+m-\frac{1}{4}$,
∵x2+x+m的值都是正数,
∴$m-\frac{1}{4}>0$,
得$m>\frac{1}{4}$.
(2)当m=-1时,x2+x-1=0,
①x2010+x2009-x2008=x2008(x2+x-1)=0;
②x3+2x2-2010=x(x2+x-1)+(x2+x-1)-2009=-2009;
点评 此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,△ABC的顶点坐标分别为A(-2,5),B(-4,3),C(-1,-1).
如图,在平面直角坐标系xOy中,△ABC的顶点坐标分别为A(-2,5),B(-4,3),C(-1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AD∥BC,∠A=∠ABC=90°,且AD=$\frac{1}{2}$CD.将梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,延长BF交AD延长线于点E,连接EC.
如图,在梯形ABCD中,AD∥BC,∠A=∠ABC=90°,且AD=$\frac{1}{2}$CD.将梯形ABCD沿对角线BD折叠,点A恰好落在CD边的点F上,延长BF交AD延长线于点E,连接EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
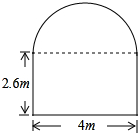 如图所示,某住宅社区在相邻两楼之间修建一个上方是一个半圆,下方是长方形的仿古通道,现有一辆卡车装满家具后,高4米,宽2.4米,请问这辆送家具的卡车能否通过这个通道?
如图所示,某住宅社区在相邻两楼之间修建一个上方是一个半圆,下方是长方形的仿古通道,现有一辆卡车装满家具后,高4米,宽2.4米,请问这辆送家具的卡车能否通过这个通道?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,点O是∠EPF平分线上的一点,以点O为圆心的圆与角的两边分别交于点A、B和C、D.
如图所示,点O是∠EPF平分线上的一点,以点O为圆心的圆与角的两边分别交于点A、B和C、D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com