
【题目】已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论中一定成立的是_____(把所有正确结论的序号都填在横线上).①DF⊥AB;②CG=2GA;③CG=DF+GE;④S四边形BFGC=![]() ﹣1.
﹣1.

【答案】①②③
【解析】
①由四边形ABCD是菱形,得出对角线平分对角,求得∠GAD=∠2,得出AG=GD,AE=ED,由SAS证得△AFG≌△AEG,得出∠AFG=∠AEG=90°,即可得出①正确;
②由DF⊥AB,F为边AB的中点,证得AD=BD,证出△ABD为等边三角形,得出∠BAC=∠1=∠2=30°,由AC=2ABcos∠BAC,AG![]() ,求出AC,AG,即可得出②正确;
,求出AC,AG,即可得出②正确;
③由勾股定理求出DF![]() ,由GE=tan∠2ED求出GE,即可得出③正确;
,由GE=tan∠2ED求出GE,即可得出③正确;
④由S四边形BFGC=S△ABC﹣S△AGF求出数值,即可得出④不正确.
∵四边形ABCD是菱形,
∴∠FAG=∠EAG,AB=AD,BC∥AD,
∴∠1=∠GAD.
∵∠1=∠2,
∴∠GAD=∠2,
∴AG=GD.
∵GE⊥AD,
∴GE垂直平分AD,
∴AE=ED.
∵F为边AB的中点,
∴AF=AE,
在△AFG和△AEG中,
∵ ,
,
∴△AFG≌△AEG(SAS),
∴∠AFG=∠AEG=90°,
∴DF⊥AB,
∴①正确;
连接BD交AC于点O.
∵DF⊥AB,F为边AB的中点,
∴AF![]() AB=1,AD=BD.
AB=1,AD=BD.
∵AB=AD,
∴AD=BD=AB,
∴△ABD为等边三角形,
∴∠BAD=∠BCD=60°,
∴∠BAC=∠1=∠2=30°,
∴AC=2AO=2ABcos∠BAC=2×2![]() 2
2![]() ,
,
AG ,
,
∴CG=AC﹣AG=2![]() ,
,
∴CG=2GA,
∴②正确;
∵GE垂直平分AD,
∴ED![]() AD=1,
AD=1,
由勾股定理得:DF![]() ,
,
GE=tan∠2ED=tan30°×1![]() ,
,
∴DF+GE![]() span>CG,
span>CG,
∴③正确;
∵∠BAC=∠1=30°,
∴△ABC的边AC上的高等于AB的一半,即为1,
FG![]() AG
AG![]() ,
,
S四边形BFGC=S△ABC﹣S△AGF![]() 2
2![]() 1
1![]() 1
1![]() ,
,
∴④不正确.
故答案为:①②③.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
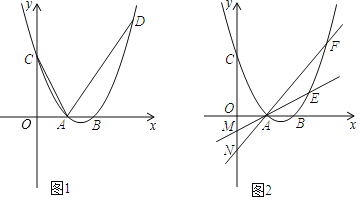
【题目】如图,抛物线y=![]() x2﹣3x+4与x轴交于A、B两点(A点在B点的左侧),交y轴于点C.
x2﹣3x+4与x轴交于A、B两点(A点在B点的左侧),交y轴于点C.
(1)A点坐标为 ,B点坐标为 ,C点坐标为 ;
(2)如图1,D为B点右侧抛物线上一点,连接AD,若tan∠CAD=2,求D点坐标;
(3)E、F是对称轴右侧第一象限抛物线上的两动点,直线AE、AF分别交y轴于M、N,如图2.若OMON=2,直线EF上有且只有一点P到原点O的距离为定值,求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.
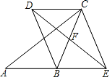
![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
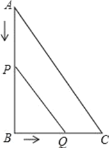
【题目】如图,在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A出发,沿边AB向终点B移动,同时点Q从点B出发,沿边BC向终点C移动.已知点P,Q的移动速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为xs.
(1)当x为何值时,四边形APQC的面积等于20![]() ?
?
(2)当x为何值时,△PBQ与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
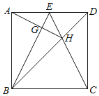
A.①③B.①②③④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种书包,平均每天可销售100件,每件盈利30元.试营销阶段发现:该商品每件降价1元,超市平均每天可多售出10件.设每件商品降价![]() 元时,日盈利为
元时,日盈利为![]() 元.据此规律,解决下列问题:
元.据此规律,解决下列问题:
(1)降价后每件商品盈利 元,超市日销售量增加 件(用含![]() 的代数式表示);
的代数式表示);
(2)在上述条件不变的情况下,求每件商品降价多少元时,超市的日盈利最大?最大为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=a与抛物线![]() 交于A、B两点(A在B的左侧),交y轴于点C
交于A、B两点(A在B的左侧),交y轴于点C
(1)若AB=4,求a的值
(2)若抛物线上存在点D(不与A、B重合),使![]() ,求a的取值范围
,求a的取值范围
(3)如图2,直线y=kx+2与抛物线交于点E、F,点P是抛物线上的动点,延长PE、PF分别交直线y=-2于M、N两点,MN交y轴于Q点,求QM·QN的值。
图1 图2
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k+1)x+k2+1=0.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且k=2,求该矩形的对角线L的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com