
【题目】在⊙O中,AB为直径,C为⊙O上一点.
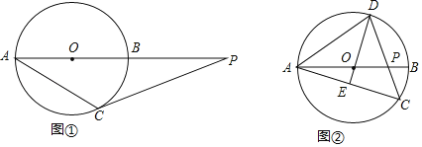
(Ⅰ)如图①,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=32°,求∠P的大小;
(Ⅱ)如图②,D为优弧ADC上一点,且DO的延长线经过AC的中点E,连接DC与AB相交于点P,若∠CAB=16°,求∠DPA的大小.
【答案】(Ⅰ)∠P=26°;(Ⅱ)∠DPA=69°
【解析】
(1)首先连接OC,由切线的性质可得OC⊥PC,由OA=OC,∠CAB=32°,即可利用三角形外角性质求得∠POC的度数,进而可得到答案;
(2)根据垂径定理的推论可得到OC⊥PC,进而可得到∠AOD=106°,根据圆周角定理得到∠C的度数,利用三角形外角性质得到答案.
解:(Ⅰ)连接OC,如图①,
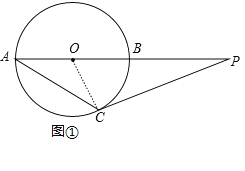
∵PC为切线,
∴OC⊥PC,
∴∠OCP=90°,
∵OA=OC,
∴∠OCA=∠CAB=32°,
∴∠POC=∠OCA+∠CAB=64°,
∴∠P=90°﹣∠POC=90°﹣64°=26°;
(Ⅱ)如图②,
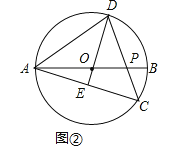
∵点E为AC的中点,
∴OD⊥AC,
∴∠OEA=90°,
∴∠AOD=∠CAB+∠OEA=16°+90°=106°,
∴∠C=![]() ∠AOD=53°,
∠AOD=53°,
∴∠DPA=∠BAC+∠C=16°+53°=69°.


科目:初中数学 来源: 题型:
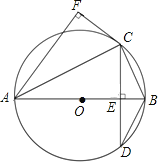
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
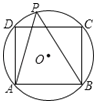
A.45° B.60° C.45° 或135° D.60° 或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是直线y=![]() +2与双曲线y=
+2与双曲线y=![]() 在第一象限内的一个交点,直线y=
在第一象限内的一个交点,直线y=![]() +2与x轴、y轴的交点分别为A、C,过P作PB⊥x轴,AB+PB=9.
+2与x轴、y轴的交点分别为A、C,过P作PB⊥x轴,AB+PB=9.
(1)求m的值;
(2)在双曲线上是否存在一点G,使得△ABG的面积等于△PBC的面积?若存在,求出点G的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
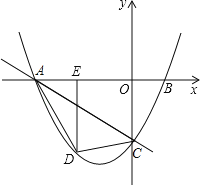
【题目】如图,直线y=-![]() x-3与x轴,y轴分别交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴的另一个交点为点B(2,0),点D是抛物线上一点,过点D作DE⊥x轴于点E,连接AD,DC.设点D的横坐标为m.
x-3与x轴,y轴分别交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴的另一个交点为点B(2,0),点D是抛物线上一点,过点D作DE⊥x轴于点E,连接AD,DC.设点D的横坐标为m.
(1)求抛物线的解析式;
(2)当点D在第三象限,设△DAC的面积为S,求S与m的函数关系式,并求出S的最大值及此时点D的坐标;
(3)连接BC,若∠EAD=∠OBC,请直接写出此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=BC=5,AB=6,求四边形AMCM的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“同享一片蓝天,共建美好家园”,北京某中学初三年级同学积极参与义务植树活动.小明同学为了了解本年级600个同学在2019年义务植树的数量,进行了抽样调查,随即抽取了其中30个同学,收集的数据如下(单位:棵)

(1)对以上数据进行整理、描述和
①绘制如下的统计图:
本年级30个同学在2019年义务植树的数量统计图
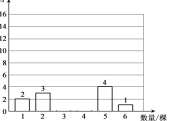
则该统计图中种植3棵树的有 个同学,种植4棵树的有 个同学
②这30个同学2019年义务植树数量的中位数是 ,众数_______;
(2)中国植树节定于每年的3月12日,是中国为激发人们爱林、造林的热情,促进国土绿化,保护人类赖以生存的生态环境.经过进一步调查,小明同学发现这30个同学中有23个是在3月份去义务植树的,由此可以估计该年级所有同学中在3月份去义务植树的有________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com