
【题目】如图,在每个小正方形边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上,
均在格点上,![]() 为
为![]() 边上的一点.
边上的一点.
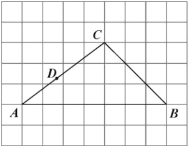
(Ⅰ)线段![]() 的值为______________;
的值为______________;
(Ⅱ)在如图所示的网格中,![]() 是
是![]() 的角平分线,在
的角平分线,在![]() 上求一点
上求一点![]() ,使
,使![]() 的值最小,请用无刻度的直尺,画出
的值最小,请用无刻度的直尺,画出![]() 和点
和点![]() ,并简要说明
,并简要说明![]() 和点
和点![]() 的位置是如何找到的(不要求证明)___________.
的位置是如何找到的(不要求证明)___________.
【答案】(Ⅰ)![]() (Ⅱ)如图,取格点
(Ⅱ)如图,取格点![]() 、
、![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() .
.
【解析】
(Ⅰ)根据勾股定理进行计算即可.
(Ⅱ)根据菱形的每一条对角线平分每一组对角,构造边长为5的菱形ABEC,连接AE交BC于M,即可得出![]() 是
是![]() 的角平分线,再取点F使AF=5,则根据等腰三角形的性质得出点C与F关于AM对称,连接DF交AM于点P,此时
的角平分线,再取点F使AF=5,则根据等腰三角形的性质得出点C与F关于AM对称,连接DF交AM于点P,此时![]() 的值最小.
的值最小.
(Ⅰ)根据勾股定理得AC=![]() ;
;
故答案为:5.
(Ⅱ)如图,如图,取格点![]() 、
、![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,则点P即为所求.
,则点P即为所求.
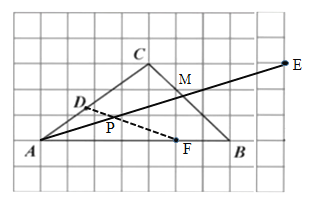
说明:构造边长为5的菱形ABEC,连接AE交BC于M,则AM即为所求的![]() 的角平分线,在AB上取点F,使AF=AC=5,则AM垂直平分CF,点C与F关于AM对称,连接DF交
的角平分线,在AB上取点F,使AF=AC=5,则AM垂直平分CF,点C与F关于AM对称,连接DF交


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=15,将△ABC绕点B顺时针旋转60°,得到△BDE,连结DC交AB于点F,则△ACF与△BDF的周长之和为( )
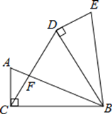
A.48B.50C.55D.60
查看答案和解析>>
科目:初中数学 来源: 题型:
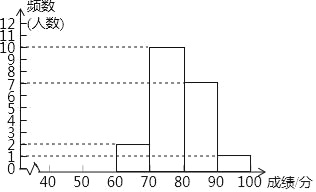
【题目】为了推动全社会自觉尊法学法守法用法,促进全面依法治国,某区每年都举办普法知识竞赛,该区某单位甲、乙两个部门各有员工200人,要在这两个部门中挑选一个部门代表单位参加今年的竞赛,为了解这两个部门员工对法律知识的掌握情况,进行了抽样调查,从甲、乙两个部门各随机抽取20名员工,进行了法律知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理,描述和分析,下面给出了部分信息.
a.甲部门成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100)
b.乙部门成绩如下:
40 52 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c.甲、乙两部门成绩的平均数、方差、中位数如下:
平均数 | 方差 | 中位数 | |
甲 | 79.6 | 36.84 | 78.5 |
乙 | 77 | 147.2 | m |
d.近五年该单位参赛员工进入复赛的出线成绩如下:
2014年 | 2015年 | 2016年 | 2017年 | 2018年 | |
出线成绩(百分制) | 79 | 81 | 80 | 81 | 82 |
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)可以推断出选择 部门参赛更好,理由为 ;
(3)预估(2)中部门今年参赛进入复赛的人数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作等腰三角形外接圆”的尺规作图过程.
已知:如图1,在![]() 中,AB=AC.
中,AB=AC.
求作:等腰![]() 的外接圆.
的外接圆.

作法:
①如图2,作![]() 的平分线交BC于D ;
的平分线交BC于D ;
②作线段AB的垂直平分线EF;
③EF与AD交于点O;
④以点O为圆心,以OB为半径作圆.
所以,![]() 就是所求作的等腰
就是所求作的等腰![]() 的外接圆.
的外接圆.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留痕迹);
(2)完成下面的证明.
![]() AB=AC,
AB=AC,![]() ,
,
![]() _________________________.
_________________________.
![]() AB的垂直平分线EF与AD交于点O,
AB的垂直平分线EF与AD交于点O,
![]() OA=OB,OB=OC
OA=OB,OB=OC
(填写理由:______________________________________)
![]() OA=OB=OC.
OA=OB=OC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某镇组织20辆汽车装运完![]() 三种品牌脐橙共100吨参加上海世博会,按计划,20辆汽车都要装运,每辆汽车只能装运用一种脐橙,且必须装满。根据下表提供的信息,解答以下问题:
三种品牌脐橙共100吨参加上海世博会,按计划,20辆汽车都要装运,每辆汽车只能装运用一种脐橙,且必须装满。根据下表提供的信息,解答以下问题:
从A,B两地运往甲,乙两地的费用如下表:
脐橙品种 | A | B | C |
每辆汽车运载量(吨) | 6 | 5 | 4 |
每吨脐橙获利(百元) | 12 | 16 | 10 |
(1)设装运![]() 种脐橙的车辆数为
种脐橙的车辆数为![]() ,装运
,装运![]() 种脐橙的车辆数为
种脐橙的车辆数为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案?
(3)若要使此次销售获利最大,应采用哪种安排方案?请求出最大利润的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 为常数,
为常数,![]() 与
与![]() 合起来的图象记为
合起来的图象记为![]() .
.
(Ⅰ)若![]() 过点
过点![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)若![]() 的顶点在直线
的顶点在直线![]() 上,求
上,求![]() 的值;
的值;
(Ⅲ)设![]() 在
在![]() 上最高点的纵坐标为
上最高点的纵坐标为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() ,连接
,连接![]() .请用等式表示线段
.请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.小明根据学习函数的经验.对线段
之间的数量关系.小明根据学习函数的经验.对线段![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于点![]() 在射线
在射线![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() ,
,![]() ,
,![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() (x>0)交于点
(x>0)交于点![]() .
.
(1)求a,k的值;
(2)已知直线![]() 过点
过点![]() 且平行于直线
且平行于直线![]() ,点P(m,n)(m>3)是直线
,点P(m,n)(m>3)是直线![]() 上一动点,过点P分别作
上一动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线,交双曲线
轴的平行线,交双曲线![]() (x>0)于点
(x>0)于点![]() 、
、![]() ,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为
,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为![]() .横、纵坐标都是整数的点叫做整点.
.横、纵坐标都是整数的点叫做整点.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;②若区域
内的整点个数;②若区域![]() 内的整点个数不超过8个,结合图象,求m的取值范围.
内的整点个数不超过8个,结合图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 内接于
内接于![]() ,弦
,弦![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
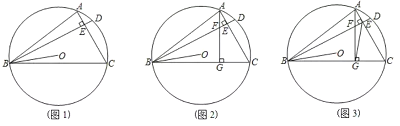
(1)如图1,求证:![]() ;
;
(2)如图2,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() 、
、![]() ,且
,且![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com