
【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:

(习题回顾)已知:如图1,在![]() 中,
中,![]() ,
,![]() 是角平分线,
是角平分线,![]() 是高,
是高,![]() 、
、![]() 相交于点
相交于点![]() .求证:
.求证:![]() ;
;
(变式思考)如图2,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的高,若
边上的高,若![]() 的外角
的外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() ,其反向延长线与
,其反向延长线与![]() 边的延长线交于点
边的延长线交于点![]() ,则
,则![]() 与
与![]() 还相等吗?说明理由;
还相等吗?说明理由;
(探究延伸)如图3,在![]() 中,
中,![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() .
.![]() 的外角
的外角![]() 的平分线所在直线
的平分线所在直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .直接写出
.直接写出![]() 与
与![]() 的数量关系.
的数量关系.
【答案】[习题回顾]证明见解析;[变式思考] 相等,证明见解析;[探究延伸] ∠M+∠CFE=90°,证明见解析.
【解析】
[习题回顾]根据同角的余角相等可证明∠B=∠ACD,再根据三角形的外角的性质即可证明;
[变式思考]根据角平分线的定义和对顶角相等可得∠CAE=∠DAF、再根据直角三角形的性质和等角的余角相等即可得出![]() =
=![]() ;
;
[探究延伸]根据角平分线的定义可得∠EAN=90°,根据直角三角形两锐角互余可得∠M+∠CEF=90°,再根据三角形外角的性质可得∠CEF=∠CFE,由此可证∠M+∠CFE=90°.
[习题回顾]证明:∵∠ACB=90°,CD是高,
∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,
∴∠B=∠ACD,
∵AE是角平分线,
∴∠CAF=∠DAF,
∵∠CFE=∠CAF+∠ACD,∠CEF=∠DAF+∠B,
∴∠CEF=∠CFE;
[变式思考]相等,理由如下:
证明:∵AF为∠BAG的角平分线,
∴∠GAF=∠DAF,
∵∠CAE=∠GAF,
∴∠CAE=∠DAF,
∵CD为AB边上的高,∠ACB=90°,
∴∠ADC=90°,
∴∠ADF=∠ACE=90°,
∴∠DAF+∠F=90°,∠E+∠CAE=90°,
∴∠CEF=∠CFE;
[探究延伸]∠M+∠CFE=90°,
证明:∵C、A、G三点共线AE、AN为角平分线,
∴∠EAN=90°,
又∵∠GAN=∠CAM,
∴∠M+∠CEF=90°,
∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,
∴∠CEF=∠CFE,
∴∠M+∠CFE=90°.


科目:初中数学 来源: 题型:
【题目】已知:以O为圆心的扇形AOB中,∠AOB=90°,点C为 ![]() 上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.
上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.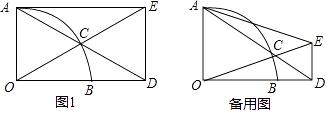
(1)如图1,当四边形AODE为矩形时,求∠ADO的度数;
(2)当扇形的半径长为5,且AC=6时,求线段DE的长;
(3)联结BC,试问:在点C运动的过程中,∠BCD的大小是否确定?若是,请求出它的度数;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2= ![]() 的图象相交于A,B两点,点B的坐标为(2m,﹣m).
的图象相交于A,B两点,点B的坐标为(2m,﹣m).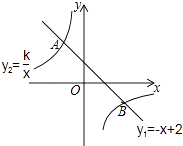
(1)求出m值并确定反比例函数的表达式;
(2)请直接写出当x<m时,y2的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y1= ![]() (a>0,a为常数)和y2=
(a>0,a为常数)和y2= ![]() 在第一象限内的图象如图所示,点M在y2=
在第一象限内的图象如图所示,点M在y2= ![]() 的图象上,MC⊥x轴于点C,交y1=
的图象上,MC⊥x轴于点C,交y1= ![]() 的图象于点A;MD⊥y轴于点D,交y1=
的图象于点A;MD⊥y轴于点D,交y1= ![]() 的图象于点B,当点M在y2=
的图象于点B,当点M在y2= ![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积为2﹣a;
③当a=1时,点A是MC的中点;
④若S四边形OAMB=S△ODB+S△OCA , 则四边形OCMD为正方形.
其中正确的是 . (把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接济川中学红歌演讲比赛,济川校区七年级(15)(16)班决定订购同一套服装,两班一共有103人(15班人数多于16班),经协商,某服装店给出的价格如下:
购买人数/人 | 1~50人 | 50~100人 | 100以上人 |
每套服装价格/元 | 50 | 45 | 40 |
例如:若购买人数为60人,则购买共需花费60×45=2700元.
(1)如果两个班都以班为单位分别购买,则一共需花费4875元,那么15,16班各有多少名学生?
(2)如果两个班联合起来,做为一个整体购买,则能节省多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为4,对角线相交于点P,顶点A,C分别在x轴,y轴的正半轴上,抛物线L经过O,P,A三点,点E是正方形内的抛物线上的动点.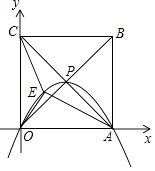
(1)点P的坐标为;
(2)求抛物线L的解析式;
(3)求△OAE与△OCE面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建国家卫生城市,需要购买甲、乙两种类型的分类垃圾桶替换原来的垃圾桶,![]() ,
,![]() ,
,![]() 三个小区所购买的数量和总价如表所示.
三个小区所购买的数量和总价如表所示.
甲型垃圾桶数量(套) | 乙型垃圾桶数量(套) | 总价(元) | |
|
|
|
|
|
|
|
|
|
|
|
|
(1)问甲型垃圾桶、乙型垃圾桶的单价分别是每套多少元?
(2)求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】福田区某轿车销售公司为龙泉工业区代销 A 款轿车,为了吸引购车族,销售公司打出降价牌,今年 5月份A款轿车每辆售价比去年同期每辆售价低 1万元,如果卖出相同数量的 A 款轿车,去年的销售额为100万元,今年销售额只有90万元.
(1)今年 5月份 A 款轿车每辆售价为多少元?
(2)为了增加收入,该轿车公司决定再为龙泉工业区代销 B款轿车,已知 A款轿车每辆进价为 7.5万元,B款轿车每辆进价为 6万元,公司预计用不多于105万元的资金购进这两款轿车共 15 辆,但A款轿车不多于6辆,试问共有几种进货方案?
(3)在⑵的条件下,B款轿车每辆售价为 8万元,为打开B款轿车的销路,公司决定每售出一辆 B款轿车,返还顾客现金a( 0<a ≤1 )万元.假设购进的15辆车能够全部卖出去,试讨论采用哪种进货方案可以使该轿车销售公司卖出这 15辆车后获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,设其面积为S,则第一步: ![]() =m;第二步:
=m;第二步: ![]() =k;第三步:分别用3、4、5乘以k,得三边长”.
=k;第三步:分别用3、4、5乘以k,得三边长”.
(1)当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;
(2)你能证明“积求勾股法”的正确性吗?请写出证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com