
���� ��1��������������ô���ʽ�ֱ��ʾ��y1��y2��
��2����a=15��a=11�ֱ���루1���еĴ���ʽ���ɽ���⣮
��� �⣺��1��������ɵã�
y1=3��400+400a��0.5=200a+1200��
y2=��a+3����400��0.6=240a+720��
��y1=200a+1200��y2=240a+720��
��2����a=15ʱ��y1=200��15+1200=4200��
y2=240��15+720=4320��
��4320��4200��
�൱a=15ʱ��ѡ��������磻
��a=11ʱ��
y1=200��11+1200=3400��
y2=240��11+720=3360��
��3360��3400��
�൱a=11ʱ��ѡ���������磮
���� ���⿼���д���ʽ������Ĺؼ�����ȷ���⣬�г���Ӧ�Ĵ���ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ����С���4λͬѧ���ڿ������������⣬ѧ��A����λ��ͼ��ʾ��ѧ��B��C��D�����������������λ�ϣ���ѧ��B����2����λ�ĸ����ǣ�������
����С���4λͬѧ���ڿ������������⣬ѧ��A����λ��ͼ��ʾ��ѧ��B��C��D�����������������λ�ϣ���ѧ��B����2����λ�ĸ����ǣ�������| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{1}{6}$ | D�� | $\frac{1}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x��Ԫ�� | 10 | 15 | 20 | �� |
| y������ | 30 | 25 | 20 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
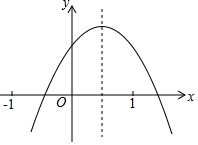 ��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��� ��a+b+c��0��a-b+c��0��b+2a��0��abc��0��5��b2��4ac��������ȷ�ĸ����ǣ�������
��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��� ��a+b+c��0��a-b+c��0��b+2a��0��abc��0��5��b2��4ac��������ȷ�ĸ����ǣ�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
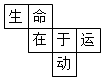 һ��������ı���չ��ͼ��ͼ��ʾ����ԭ���������֡�����������Ķ�����������ǣ�������
һ��������ı���չ��ͼ��ͼ��ʾ����ԭ���������֡�����������Ķ�����������ǣ�������| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
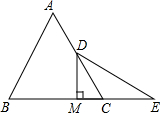 ��ͼ����֪�ڵȱ�������ABC�У�D��M�ֱ���AC��BE���е㣬EΪBC�ӳ�����һ�㣬��CE=CD����֤��DM��BC��
��ͼ����֪�ڵȱ�������ABC�У�D��M�ֱ���AC��BE���е㣬EΪBC�ӳ�����һ�㣬��CE=CD����֤��DM��BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com