
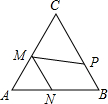
 如图,在等边△ABC中,AB=4,P、M、N分别是BC,CA、AB边上动点,则PM+MN的最小值是
如图,在等边△ABC中,AB=4,P、M、N分别是BC,CA、AB边上动点,则PM+MN的最小值是科目:初中数学 来源: 题型:
 用一个长60米的篱笆围成一个长方形鸡场(鸡场的一边靠墙,墙长为20米),如图,若BC=2AB,求AB和BC的长,并检验是否符合要求;若不符合要求,提出改进意见,并求出改进后的AB、BC的长,仍满足(BC=2AB).
用一个长60米的篱笆围成一个长方形鸡场(鸡场的一边靠墙,墙长为20米),如图,若BC=2AB,求AB和BC的长,并检验是否符合要求;若不符合要求,提出改进意见,并求出改进后的AB、BC的长,仍满足(BC=2AB).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| m-3 |
| x |
| A、m>3 | B、m<3 |
| C、m>-3 | D、m<-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
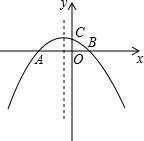 如图,抛物线y=-
如图,抛物线y=-| 1 |
| 9 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 水位变化/米 | +0.25 | +0.52 | -0.18 | +0.06 | -0.13 | -0.49 | +0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
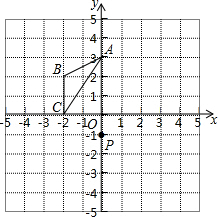 如图,△ABC的位置如图,
如图,△ABC的位置如图,查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰△ABC中,AB=AC,BC∥x轴,点A.C在反比例函数y=
如图,等腰△ABC中,AB=AC,BC∥x轴,点A.C在反比例函数y=| 4 |
| x |
| 1 |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com