
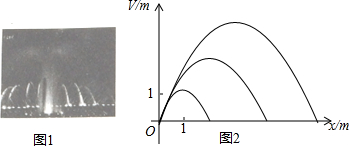
分析 (1)由题意抛物线的顶点坐标为(3,3),根据顶点坐标公式可得$\left\{\begin{array}{l}{-\frac{b}{2a}=3}\\{\frac{-{b}^{2}}{4a}=3}\end{array}\right.$,由此即可解决问题.
(2)判断出顶点坐标,即可解决问题.
(3)根据抛物线的对称轴的位置,列出不等式,求出b的取值范围$\frac{36}{7}$≤b≤$\frac{39}{7}$,当b=$\frac{39}{7}$时,抛物线的顶点坐标($\frac{39}{4}$,$\frac{1521}{56}$),此时$\frac{1521}{56}$=$\frac{39}{4}$k,解得k=$\frac{39}{14}$,
当b=$\frac{36}{7}$时,抛物线的顶点坐标为(9,$\frac{162}{7}$),此时$\frac{162}{7}$=9k,解得k=$\frac{18}{7}$,由此可得k的取值范围为$\frac{18}{7}$≤k$≤\frac{39}{14}$.
解答 解:(1)由题意抛物线的顶点坐标为(3,3),
∴$\left\{\begin{array}{l}{-\frac{b}{2a}=3}\\{\frac{-{b}^{2}}{4a}=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=2}\end{array}\right.$,
∴a=-$\frac{1}{3}$,b=2.
(2)由题意抛物线的对称轴x=9,
∵顶点在直线y=x上,
∴顶点坐标为(9,9),
∴此时喷出的抛物线水线最大高度为9米.
(3)由题意9≤-$\frac{b}{2a}$≤$\frac{39}{4}$,
∴9≤$\frac{7}{4}$≤$\frac{39}{4}$,
∴$\frac{36}{7}$≤b≤$\frac{39}{7}$,
当b=$\frac{39}{7}$时,抛物线的顶点坐标($\frac{39}{4}$,$\frac{1521}{56}$),此时$\frac{1521}{56}$=$\frac{39}{4}$k,解得k=$\frac{39}{14}$,
当b=$\frac{36}{7}$时,抛物线的顶点坐标为(9,$\frac{162}{7}$),此时$\frac{162}{7}$=9k,解得k=$\frac{18}{7}$,
∴k的取值范围为$\frac{18}{7}$≤k$≤\frac{39}{14}$.
点评 本题考查二次函数的应用、一次函数的应用等知识,解题的关键是灵活运用为二次函数的性质解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运输工具 | 平均速度(千米/小时) | 运费(元/千米) | 装卸总费用(元) |
| 火车 | 120 | 20 | 2400 |
| 汽车 | 100 | 25 | 1600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com