
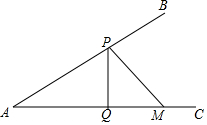
 如图,∠BAC=30°,M为AC上一点,AM=2,点P是AB上的一动点,PQ⊥AC,垂足为点Q,则PM+PQ的最小值为$\sqrt{3}$.
如图,∠BAC=30°,M为AC上一点,AM=2,点P是AB上的一动点,PQ⊥AC,垂足为点Q,则PM+PQ的最小值为$\sqrt{3}$. 分析 本题作点M关于AB的对称点N,根据轴对称性找出点P的位置,如图,根据三角函数求出MN,∠N,再根据三角函数求出结论.
解答 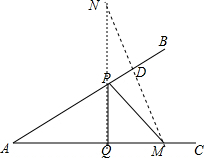 解:作点M关于AB的对称点N,过N作NQ⊥AC于Q交AB于P,
解:作点M关于AB的对称点N,过N作NQ⊥AC于Q交AB于P,
则NQ的长即为PM+PQ的最小值,
连接MN交AB于D,则MD⊥AB,DM=DN,
∵∠NPB=∠APQ,
∴∠N=∠BAC=30°,
∵∠BAC=30°,AM=2,
∴MD=$\frac{1}{2}$AM=1,
∴MN=2,
∴NQ=MN•cos∠N=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查含30°直角三角形的性质、轴对称--最短路线问题及三角函数,正确确定P点的位置是解题的关键.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:选择题
| 金额/元 | 5 | 10 | 20 | 50 | 100 |
| 人数 | 4 | 16 | 15 | 9 | 6 |
| A. | 10,20.6 | B. | 20,20.6 | C. | 10,30.6 | D. | 20,30.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1尾 | B. | 50尾 | C. | 500尾 | D. | 1 000尾 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
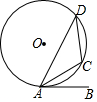 如图,$\widehat{AC}$=$\widehat{DC}$,AC平分∠DAB.
如图,$\widehat{AC}$=$\widehat{DC}$,AC平分∠DAB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 组别 | 正确字数x | 人数 |
| A | 0≤x<8 | 10 |
| B | 8≤x<16 | 15 |
| C | 16≤x<24 | 25 |
| D | 24≤x<32 | m |
| E | 32≤x<40 | n |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com