
 如图,直线 y=-2x+4与坐标轴分别交于B、D,四边形ABCD为菱形,其对角线交于点P,AC交y轴于点E.
如图,直线 y=-2x+4与坐标轴分别交于B、D,四边形ABCD为菱形,其对角线交于点P,AC交y轴于点E.分析 (1)根据一次函数图象上点的坐标特征即可求得B、D的坐标,然后通过根据菱形的性质证得∴△ABP∽△DBO,即可求得AB=5,即可求得C的坐标;
(2)证得∴△PDE∽△ODB,即可求得PE的长.
解答 解:(1)∵直线 y=-2x+4与坐标轴分别交于B、D,
∴当y=0时,x=2,当x=0时,y=4,
∴B(2,0),D(0,4),
∴BD=$\sqrt{O{B}^{2}+O{D}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵四边形ABCD为菱形,
∴PB=PD=$\frac{1}{2}$BD=$\sqrt{5}$,AC⊥BD,
∴∠APB=∠DOB=90°,
∵∠ABP=∠DBO,
∴△ABP∽△DBO,
∴$\frac{AB}{BD}$=$\frac{PB}{OB}$,即$\frac{AB}{2\sqrt{5}}$=$\frac{\sqrt{5}}{2}$,
∴AB=5,
∴OA=AB-OB=5-2=3,
∴A(-3,0);
(2)∵∠DPE=∠DOB=90°,∠PDE=∠ODB,
∴△PDE∽△ODB,
∴$\frac{PE}{OB}$=$\frac{PD}{OD}$,即$\frac{PE}{2}$=$\frac{\sqrt{5}}{4}$,
∴PE=$\frac{\sqrt{5}}{2}$.
点评 本题考查了一次函数图象上点的坐标 特征,菱形的性质,三角形相似的判定和性质以及勾股定理的应用等,熟练掌握性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
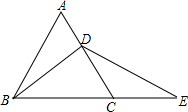 如图所示,△ABC为等边三角形,BD为中线,延长BC至E,使 DE=BD.
如图所示,△ABC为等边三角形,BD为中线,延长BC至E,使 DE=BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm.
在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A、B在数轴上,它们所对应的数分别是$\frac{2}{x-2}$和$\frac{1-x}{2-x}$.
如图,点A、B在数轴上,它们所对应的数分别是$\frac{2}{x-2}$和$\frac{1-x}{2-x}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OP是∠AOB的平分线,点P到OA的距离为3,点N是OB上的任意一点,则线段PN的取值范围为( )
如图,OP是∠AOB的平分线,点P到OA的距离为3,点N是OB上的任意一点,则线段PN的取值范围为( )| A. | PN<3 | B. | PN>3 | C. | PN≥3 | D. | PN≤3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com