练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
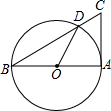
    3．如图，AB是⊙O的直径，AC切⊙O于A，BC交⊙O于点D，若∠C=70°，则∠AOD的度数为（　　）
    A．70°B．35°C．20°D．40°

    分析 先依据切线的性质求得∠CAB的度数，然后依据直角三角形两锐角互余的性质得到∠CBA的度数，然后由圆周角定理可求得∠AOD的度数．

    解答 解：∵AC是圆O的切线，AB是圆O的直径，
    ∴AB⊥AC．
    ∴∠CAB=90°．
    又∵∠C=70°，
    ∴∠CBA=20°．
    ∴∠DOA=40°．
    故选：D．

    点评 本题主要考查的是切线的性质、圆周角定理、直角三角形的性质，求得∠CBA=20°是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

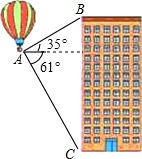    13．热气球的探测器显示，从热气球所在位置A处看一栋楼顶部B处的仰角为35°，看这栋楼底部C处的俯角为61°，已知这栋楼BC的高度为300m，求热气球所在位置距地面的距离（结果保留整数）．（参考数据：tan35°≈0.70，tan61°≈1.80）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．掷一枚硬币，正面向上是不确定事件，当抛掷次数足够多时，发现正面朝上的频率的值稳定在$\frac{1}{2}$附近，则硬币正面向上发生的可能性为$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

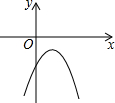    11．已知二次函数y=-（x-a）2-b的图象如图所示，则反比例函数y=$\frac{ab}{x}$与一次函数y=ax+b的图象可能是（　　）
    A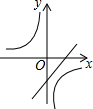．B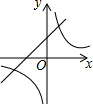．C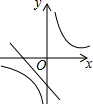．D．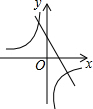

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

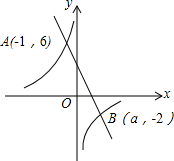    18．如图，一次函数y1=kx+b（k≠0）和反比例函数y2=$\frac{m}{x}$（m≠0）的图象交于点A（-1，6），B（a，-2）．
    （1）求一次函数与反比例函数的解析式；
    （2）根据图象直接写出y1＞y2时，x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

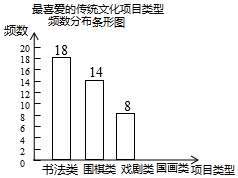    8．某校为更好地开展“传统文化进校园”活动，随机抽查了部分学生，了解他们最喜爱的传统文化项目类型（分为书法、围棋、戏剧、国画共4类），并将统计结果绘制成如图不完整的频数分布表及频数分布条形图．
    最喜爱的传统文化项目类型频数分布表
    项目类型频数频率
    书法类18a
    围棋类140.28
    喜剧类80.16
    国画类b0.20
    根据以上信息完成下列问题：
    （1）直接写出频数分布表中a的值；
    （2）补全频数分布条形图；
    （3）若全校共有学生1500名，估计该校最喜爱围棋的学生大约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．若一个三角形的两边长分别为3和7，则第三边长可能是（　　）
    A．6B．3C．2D．11

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．从今年起，我市生物和地理会考实施改革，考试结果以等级形式呈现，分A、B、C、D四个等级．某校八年级为了迎接会考，进行了一次模拟考试，随机抽取部分学生的生物成绩进行统计，绘制成如下两幅不完整的统计图．

    （1）这次抽样调查共抽取了50名学生的生物成绩．扇形统计图中，D等级所对应的扇形圆心角度数为36°；
    （2）将条形统计图补充完整；
    （3）如果该校八年级共有600名学生，请估计这次模拟考试有多少名学生的生物成绩等级为D？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在⊙O中，弦AB=3，将AB绕点O逆时针旋转60°得弦A′B′，连接OA′，已知OA′⊥AB于C，求⊙O的半径．

    查看答案和解析>>

    同步练习册答案