练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，∠CAD和∠CBD的平分线相交于点P．设∠CAD、∠CBD、∠C、∠D的度数依次为a、b、c、d，用仅含其中2个字母的代数式来表示∠P的度数：_____．

    【答案】

    【解析】

    根据三角形外角的性质可表示出：∠BFC=∠PAC+∠P，∠AFP=∠PBC+∠C，根据对顶角相等的性质，可得到∠BFC=∠AFP，从而可以用含有a、b、c、d的式子表示∠P，从而不难求解．

    ∵∠BFA=∠PAC+∠P，∠BFA=∠PBC+∠C，

    ∴∠PAC+∠P=∠PBC+∠C，

    ∵∠CAD、∠CBD、∠C、∠D的度数依次为a、b、c、d，∠CAD和∠CBD的平分线相交于点P，

    ∴a+∠P=b+c ①，

    同理：b+∠P=a+d ②，

    ①式+②式，得.2∠P=c+d，∴∠P=，

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c的图象如图所示，则点（b， ）在第（ ）象限．
    A.一
    B.二
    C.三
    D.四

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=x2﹣3x+ 与x轴相交于A、B两点，与y轴相交于点C，点D是直线BC下方抛物线上一点，过点D作y轴的平行线，与直线BC相交于点E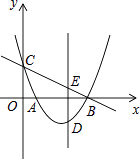
    （1）求直线BC的解析式；
    （2）当线段DE的长度最大时，求点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料
    【材料一】按一定顺序排列的一列数称为数列，记作：{an}（n属于正整数）．数列中的每一个数都叫做这个数列的项，排在第一位的数称为这个数列的第l项
    （通常也叫做首项），记作：al；排在第二位的数称为这个数列的第2项，记作：a2；…；排在第打位的数称为这个数列的第n项，记作：an ．
    【材料二】如果一个数列从第二项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列．这个常数叫做等差数列的公差，公差常用字母d表示．
    例如：数列l0，l5，20，25是等差数列．
    如果数列al ， a2 ， a3 ， …，an ， …是等差数列，那么a2﹣al=d，a3﹣a2=d，…，
    an﹣an﹣l=d．即：a2=al+d，a3=a2+d=al+d+d=al+2d，a4=a3+d=al+3d，…．
    根据上述材料，解答问题
    （1）下列数列属于等差数列的是 （只填序号）．
    ①l，2，3，4，5．②2，4，6，8，10，11．③l，1，1，1，1．
    （2）已知数列{an}是等差数列，
    ①al=1，a2=4，a3=7，…．则al0= ．
    ②首项a1=23，公差d=2，则an= ．
    （3）已知等差数列{an}满足a2=0，a6+a8=﹣10．求an ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某车间有60个工人，生产甲、乙两种零件，每人每天平均能生产甲种零件24个或乙种零件12个．已知每2个甲种零件和3个乙种零件配成一套，问应分配多少人生产甲种零件，多少人生产乙种零件，才能使每天生产的这两种零件刚好配套？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB=AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F．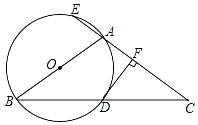
    （1）试说明DF是⊙O的切线；
    （2）若AC=3AE，求 的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一坐标系中，一次函数y=ax+2与二次函数y=x2+a的图象可能是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将菱形纸片ABCD折叠，使点A恰好落在菱形的对称中心O处，折痕为EF，若菱形ABCD的边长为2cm，∠A=120°，则EF=cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【定义】已知P为△ABC所在平面内一点，连接PA，PB，PC，在△PAB，△PBC和△PAC中，若存在一个三角形与△ABC相似（全等除外），那么就称P为△ABC的“共相似点”，根据“共相似点”是否落在三角形的内部，边上或外部，可将其分为“内共相似点”，“边共相似点”或“外共相似点”．
    （1）据定义可知，等边三角形（填“存在”或“不存在”）共相似点．
    （2）如图1，若△ABC的一个边共相似点P与其对角顶点B的连线，将△ABC分割成的两个三角形恰与原三角形均相似，试判断△ABC的形状，并说明理由．

    （3）如图2，在△ABC中，∠A＜∠B＜∠C，高线CD与角平分线BE交于点P，若P是△ABC的一个内共相似点，试说明点E是△ABC的边共相似点，并直接写出∠A的度数．

    （4）如图3，在Rt△ABC中，∠C=90°，∠A=30°，BC= ，若△PBC与△ABC相似，则满足条件的P点共有个，顺次连接所有满足条件的P点而围成的多边形的周长为 ．

    查看答案和解析>>

    同步练习册答案