
【题目】(本题10分)如图,直线y=x+m和抛物线y=![]() +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),
B(3,2).
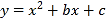
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:
(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶10分钟后,甲、乙两人相距多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
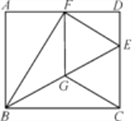
【题目】如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,将线段EF绕点F旋转,使点E落在BE上的点G处,连接CG.
(1)证明:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积;
(3)试探究当线段AB与BC满足什么数量关系时,BG=CG,请写出你的探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节约是中华民族的传统美德.为倡导市民节约用水的意识,某市对市民用水实行“阶梯收费”,制定了如下用水收费标准:每户每月的用水不超过![]() 立方米时,水价为每立方米
立方米时,水价为每立方米![]() 元,超过
元,超过![]() 立方米时,超过的部分按每立方米
立方米时,超过的部分按每立方米![]() 元收费.
元收费.
(1)该市某户居民9月份用水![]() 立方米(
立方米(![]() ),应交水费
),应交水费![]() 元,请你用含
元,请你用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)如果某户居民12月份交水费![]() 元,那么这个月该户居民用了多少立方米水?
元,那么这个月该户居民用了多少立方米水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日,是第23个世界读书日.为了推进中华传统文化教育,营造浓厚的读书氛围,我市某学校举办了“让读书成为习惯,让书香溢病校园”主题活动.为了解学生每周阅读时间,该校随机抽取了部分学生进行调查,根据调查结果,将阅诙时间![]() (单位:小时)分成了
(单位:小时)分成了![]() 组,
组, ![]()
![]()
![]() ,下图是根据这组数据绘制的两幅不完整的统计图.请你结合图中所给信息解答下列问题:
,下图是根据这组数据绘制的两幅不完整的统计图.请你结合图中所给信息解答下列问题:

(1)这次随机抽取了 名学生进行调查;
(2)补全频数分布直方图;
(3)计算扇形统计图中扇形![]() 的圆心角的度数;
的圆心角的度数;
(4)若该校共有![]() 名学生,请你估计每周阅读时间不足
名学生,请你估计每周阅读时间不足![]() 小时的学生共有多少名?
小时的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】希腊数学家丢番图(公元3-4世纪)的墓碑上记载着: “他生命的六分之一是幸福的童年;再活了他生命的十二分之一,两颊长起了细细的胡须;他结了婚,又度过了一生的七分之一;再过五年,他有了儿子,感到很幸福;可是儿子只活了他父亲全部年龄的一半;儿子死后,他在极度悲痛中度过了四年,也与世长辞了.”
根据以上信息,请你算出:
(1)丢番图的寿命;
(2)丢番图开始当爸爸时的年龄;
(3)儿子死时丢番图的年龄.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N.
(1)写出点C的坐标;
(2)求证:MD=MN;
(3)连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下面由火柴棒拼出的一系列的图形中,第n个图形由n个正方形组成.
 ……
……
(1)第2个图形中,火柴棒的根数是________.
(2)第3个图形中,火柴棒的根数是________.
(3)第n个图形中,火柴棒的根数是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
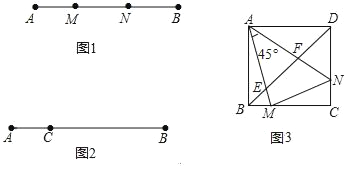
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4求BN的长;
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可);
(3)如图3,正方形ABCD中,M,N分别在BC,DC上,且BM≠DN,∠MAN=45°,AM,AN分别交BD于E,F.
求证:①E、F是线段BD的勾股分割点;
②△AMN的面积是△AEF面积的两倍.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com