
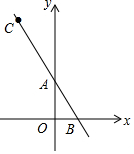 如图,过点C(-2,5)的直线AB分别交坐标轴于A(0,2),B两点,则tan∠OAB=( )
如图,过点C(-2,5)的直线AB分别交坐标轴于A(0,2),B两点,则tan∠OAB=( )| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
分析 利用待定系数法求得直线AB的解析式,然后求得B的坐标,进而利用正切函数定义求解.
解答 解:设直线AB的解析式是y=kx+b,
根据题意得:$\left\{\begin{array}{l}{-2k+b=5}\\{b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=2}\end{array}\right.$,
则直线AB的解析式是y=-$\frac{3}{2}$x+2.
在y=-$\frac{3}{2}$x+2中令y=0,解得x=$\frac{4}{3}$.
则B的坐标是($\frac{4}{3}$,0),即OB=$\frac{4}{3}$.
则tan∠OAB=$\frac{OB}{OA}$=$\frac{\frac{4}{3}}{2}$=$\frac{2}{3}$.
故选B.
点评 本题考查了三角函数的定义以及待定系数法求函数解析式,正确求得B的坐标是关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
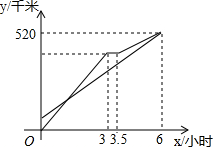 甲、乙两车从A地出发沿同一路线驶向B地,甲车匀速驶向B地,甲车出发30分钟后,乙车才出发,乙先匀速行驶一段时间后,到达货站装货后继续行驶,速度减少了56千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法中正确的是( )
甲、乙两车从A地出发沿同一路线驶向B地,甲车匀速驶向B地,甲车出发30分钟后,乙车才出发,乙先匀速行驶一段时间后,到达货站装货后继续行驶,速度减少了56千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法中正确的是( )| A. | 甲车从A地到B地行驶了6小时 | |
| B. | 甲的速度是120千米/时 | |
| C. | 乙出发90分钟追上甲 | |
| D. | 当两车在行驶过程中,相距40千米时,x=2或3.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
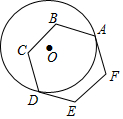 如图,半径为1的⊙O与正六边形ABCDEF相切于点A、D,则$\widehat{AD}$的长为( )
如图,半径为1的⊙O与正六边形ABCDEF相切于点A、D,则$\widehat{AD}$的长为( )| A. | $\frac{1}{6}$π | B. | $\frac{1}{3}$π | C. | $\frac{2}{3}$π | D. | $\frac{5}{6}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,则∠A1=32°;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线相交于点An,要使∠An的度数为整数,则n的值最大为6.
如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,则∠A1=32°;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线相交于点An,要使∠An的度数为整数,则n的值最大为6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
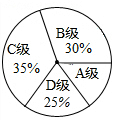 为了解某区3600名九年级学生的体育训练情况,随机抽取了区内200名九年级学生进行了一次体育模拟测试,把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如图所示的统计图,由此估计全区九年级体育测试成绩可以达到优秀的人数约为360人.
为了解某区3600名九年级学生的体育训练情况,随机抽取了区内200名九年级学生进行了一次体育模拟测试,把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如图所示的统计图,由此估计全区九年级体育测试成绩可以达到优秀的人数约为360人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com