
【题目】矩形ABCD中,AC、BD相交于O,AE平分∠BAD交BC于E.
(1)求证:△ABE是等腰直角三角形;
(2)若∠CAE=15°,求证:△ABO是等边三角形;
(3)在(2)的条件下,求∠BOE的度数.
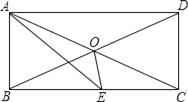
【答案】(1)证明见解析;(2)证明见解析;(3)∠BOE=75°.
【解析】分析:(1)由矩形的性质和角平分线的性质得出△ABE是等腰直角三角形;
(2)由矩形的性质得出OA=OB,再由角的和差关系可得∠AOB=60°,即可得出结论;
(3)由(2)的结论得出∠OBE=30°,证出OB=BE,求出∠BOE的度数即可.
详解:(1)∵四边形ABCD是矩形,∴∠BAD=∠ABE=90°.
∵AE平分∠BAD,∴∠BAE=45°,∴△ABE是等腰直角三角形;
(2)∵四边形ABCD是矩形,∴OA=OB.
∵∠CAE=15°,∴∠BAO=45°+15°=60°,∴△AOB是等边三角形;
(3)由(2)得:△AOB是等边三角形,∴∠ABO=60°,∴∠OBE=90°﹣60°=30°.
∵BE=AB,OB=AB,∴OB=BE,∴∠BOE=![]() (180°﹣30°)=75°.
(180°﹣30°)=75°.


科目:初中数学 来源: 题型:
【题目】如图,已知直线y= ![]() x﹣2与x轴交于点A,与y轴交于点C,经过A、C两点的抛物线与轴交于另一点B(1,0).
x﹣2与x轴交于点A,与y轴交于点C,经过A、C两点的抛物线与轴交于另一点B(1,0).
(1)求该抛物线的解析式.
(2)在直线y= ![]() x﹣2上方的抛物线上存在一动点D,连接AD、CD,设点D的横坐标为m,△DCA的面积为S,求S与m的函数关系式,并求出S的最大值.
x﹣2上方的抛物线上存在一动点D,连接AD、CD,设点D的横坐标为m,△DCA的面积为S,求S与m的函数关系式,并求出S的最大值.
(3)在抛物线上是否存在一点M,使得以M为圆心,以 ![]() 为半径的圆与直线AC相切?若存在,请求出点M的坐标;若不存在,请说明理由.
为半径的圆与直线AC相切?若存在,请求出点M的坐标;若不存在,请说明理由.
(4)在y轴的正半轴上存在一点P,使∠APB的值最大,请直接写出当∠APB最大时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD. 
(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若AB=9,BC=6.求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板按如图放置,则下列结论:
①如果∠2=30°,则有AC∥DE;
②∠BAE+∠CAD =180°;
③如果BC∥AD,则有∠2=45°;
④如果∠CAD=150°,必有∠4=∠C;
正确的有( )
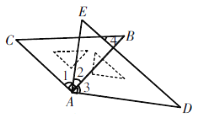
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
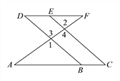
【题目】如图,E点为DF上的点,B为AC上的点,![]() ,
,![]() ,求证:DF∥AC.
,求证:DF∥AC.
证明:∵ ![]() (已知),∠1=∠3,∠2=∠4( ),
(已知),∠1=∠3,∠2=∠4( ),
∴∠3=∠4(等量代换).
∴__________![]() __________( ).
__________( ).
∴∠C=∠ABD( ).
∵∠C=∠D( ),
∴∠D=__________( ).
∴AC∥DF( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
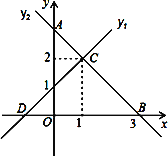
【题目】如图,直线y1与y2相交于点C(1,2),y1与x轴交于点D,与y轴交于点(0,1);y2与x轴交于点B(3,0),与y轴交于点A.下列说法正确的有_____________.
①y1的解析式为y1=x+2②OA=OB③∠CDB=45°④△AOB≌△BCD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为( )

A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠C=90°,AB的垂直平分线MN交BC于点D.
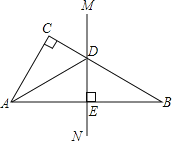
(1)如果∠CAD=20°,求∠B的度数;
(2)如果∠CAB=50°,求∠CAD的度数;
(3)如果∠CAD:∠DAB=1:2,求∠CAB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com