
分析 (1)原式第一项利用乘方的意义化简,第二项化为最简二次根式,第三项利用特殊角的三角函数值及绝对值的代数意义化简,最后一项利用零指数幂法则计算即可得到结果;
(2)首先根据题意可得分式方程$\frac{3-x}{2-x}$-$\frac{1}{x-2}$=3,解此分式方程即可求得答案,注意分式方程需检验.
解答 解:(1)-24-$\sqrt{12}$+|1-4sin60°|+(π-$\frac{2}{3}$)0
=-16-2$\sqrt{3}$+2$\sqrt{3}$-1+1
=-16;
(2)根据题意得:$\frac{3-x}{2-x}$-$\frac{1}{x-2}$=3方程两边同乘以2-x,
得:3-x+1=3(2-x),
解得x=1.
检验:当x=1时,2-x=1≠0,即x=1是原方程的解,
即当x=1时,分式$\frac{3-x}{2-x}$的值比分式$\frac{1}{x-2}$的值大3.
点评 此题考查了分式方程的应用.此题比较简单,注意掌握转化思想的应用,注意解分式方程一定要验根.同时考查了实数的运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这200名考生是总体的一个样本 | B. | 近3千名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 200名学生是样本容量 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
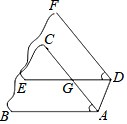 如图,某同学剪了两片角度均为50°的硬板纸纸片(∠BAC=∠EDF=50°),将其中一片平移,连结AD,如果△AGD中有两个角相等,则∠GAD的度数为50°或80°或65°.
如图,某同学剪了两片角度均为50°的硬板纸纸片(∠BAC=∠EDF=50°),将其中一片平移,连结AD,如果△AGD中有两个角相等,则∠GAD的度数为50°或80°或65°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{a}+\frac{2}{b}=\frac{3}{a+b}$ | B. | $\frac{ab}{{ab-{b^2}}}=\frac{a}{a-b}$ | C. | $\frac{2}{2a+b}=\frac{1}{a+b}$ | D. | $\frac{a}{-a+b}=-\frac{a}{a+b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com