
【题目】如图,在△ACE中,AC=CE,⊙O经过点A,C,且与边AE,CE分别交于点D,F,点B是劣弧AC上的一点,且![]() ,连接AB,BC,CD.
,连接AB,BC,CD.
(1)求证:△CDE≌△ABC;
(2)填空:若AC为⊙O的直径,则当△ACE的形状为 时,四边形ABCD为正方形.
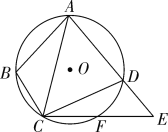
【答案】(1)证明见解析;(2)等腰直角三角形
【解析】
(1)先判断出∠BAC=∠DCE,进而得出∠CDE=∠ABC,即可得出结论;
(2)先判断出AD=CD,∠ADC=90°,进而得出∠ACD=45°,再判断出∠DCE=∠ACD=45°,即可得出∠ACE=90°,即可得出结论
(1)∵![]() ,
,
∴∠BAC=∠DCE,
∵∠CDE是圆内接四边形ABCD的外角,
∴∠CDE=∠ABC,
在△CDE和△ABC中,
 ,
,
∴△CDE≌△ABC(AAS);
(2)∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ACD=45°,
∵AC=CE,CD⊥AE,
∴∠DCE=∠ACD=45°,
∴∠ACE=90°,
∵AC=CE,
∴△ACE是等腰直角三角形.
故答案为:等腰直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
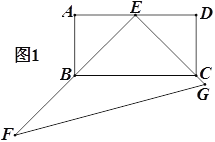
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
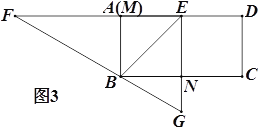
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与x轴交于A,B两点,与y轴交于点C,对称轴与x轴交于点D,若点P为y轴上的一个动点,连接PD,则
的图象与x轴交于A,B两点,与y轴交于点C,对称轴与x轴交于点D,若点P为y轴上的一个动点,连接PD,则![]() 的最小值为________.
的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
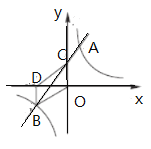
【题目】如图,在平面直角坐标系中,一次函数![]()
![]() 的图像与反比例函数
的图像与反比例函数![]()
![]() 的图像交于第一、三象限内的
的图像交于第一、三象限内的![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() ,
,![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求该反比例函数和一次函数的解析式;
(3)连接![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字;再如,(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a﹣b)4的展开式,(a﹣b)4=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
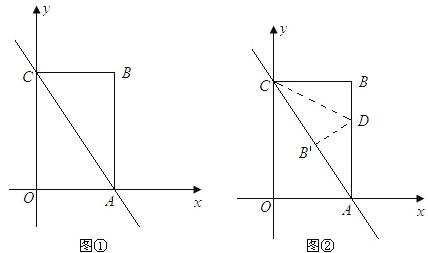
(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家所在居民楼的对面有一座大厦AB,高为74米,为测量居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
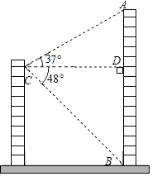
(1)求∠ACB的度数;
(2)求小明家所在居民楼与大厦之间的距离.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,cos48°≈
,cos48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
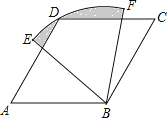
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com